《初心者~中級者向け》
今回はユニットの「増殖」について解説します。
「増殖」は前回までに解説した「分割」と合わせて「分割・増殖」とセットで扱われることが多いパース関連の知識です。
「分割」については以下の記事を参照して下さい。
▼前々回記事:「分割の基礎編」はこちらから
▼前回記事:3等分割以上の分割については「分割 応用編」で解説しています
「分割」は1つのユニットを複数に分ける知識でしたが、「増殖」はその逆で1つのユニットを増やしていく知識です。
「増殖」を使えば、決まったサイズのユニットをパース上にどんどん増やしていくことができます。
例えば「全体のサイズはわからないが、単体のパネルの大きさが決まっていて、それと同じパネルを奥に10枚並べたい」というような場合に「増殖」を使います。
「増殖」は「分割」と合わせて知っていると色々と使い勝手のよい知識です。
※本ブログの記事には広告が表示されます。
今回の授業内容と難易度
それでは、今回の記事の内容です。
まず「増殖」と「分割」はどう違うのかについて説明します。
「分割」も「増殖」も、四角形(平行四辺形)の性質を使って同じサイズのユニットをパース上に作るという点ではとても似ています。
ただ、描く手順や考え方自体は逆になりますので、「分割」と「増殖」がどのように違うのかをしっかりと理解した上で実用的な知識として身につけておきましょう。
- 難易度 2:★★☆☆☆
- 重要度 3:★★★☆☆
- 画力向上度 2:★★☆☆☆
「増殖」は「分割」が理解できていれば、それほど難しいものではありません。
1を2に増やす方法を知っていれば、あとは同じ手順で3つ、4つ…と簡単に増やしていくことができます。
絵を描いていると使う機会は色々とあるので「分割」と「増殖」はセットでおぼえておきましょう。
「分割」と「増殖」の違い
「増殖」の説明に入る前に、「分割」と「増殖」がどのように違うのかを知っておきましょう。
こちらの図は、同じサイズの板に4等分割線を入れたものです。
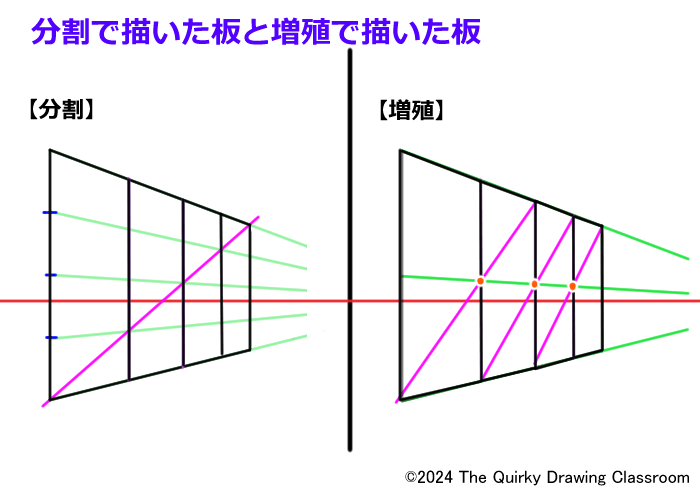
ただ、描いた方法が異なり、左側の板は「分割」を、右は「増殖」を使って描いています。
最終的に完成するものが同じならどちらでも良いように思いますが、「分割」で描くか「増殖」で描くかは「何から描きはじめるか?」で変わってきます。
はじめに大きさが決まっているユニットを必要な数に分けるのが「分割」であったのに対し、基準となる単体のユニットの大きさが決まっていて、それを必要な数に増やすのが「増殖」です。
少し難しいと思うので、平面図で図解してみましょう。
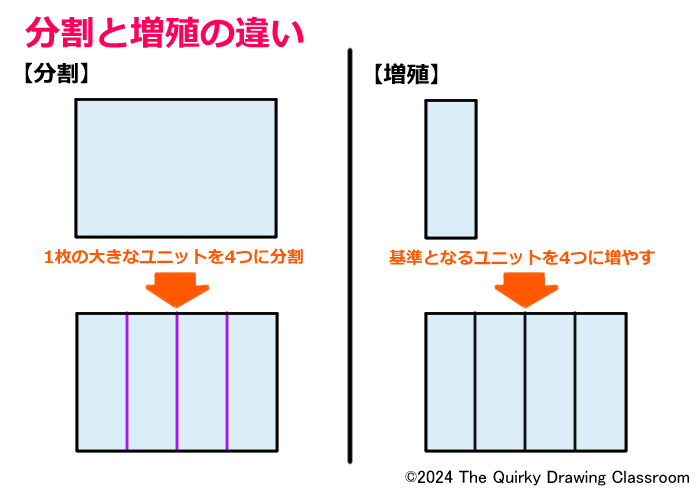
左は「分割」の考え方、右は「増殖」の考え方です。
「増殖」は基準となるユニットをどんどん増やしていくという描き方になります。
「増殖」の考え方と方法
では、「増殖」でユニットを増やす方法について解説します。
以下で、ユニットを2つに増やす方法と3つに増やす方法を例に説明していきます。
「増殖」の考え方
ユニットを増やす時の理屈は知ってしまえば、かなり簡単です。
まず「どうやって増やすのか?」という考え方から説明していきます。
「増殖」について考える時も思い出すべきはやはり平行四辺形の持つ性質です。
「分割」の時にも使った「平行四辺形(長方形)の対角線の交点(中点)を通る直線はその四角形の面積を2等分する」という平行四辺形の性質を「増殖」でも使います。
「分割」ではユニットを分けるために対角線を使いましたが、「増殖」ではユニットを増やすために使います。
同じ大きさのユニットを増やす考え方は、わかりやすいと思うので平面図で説明します。
ここで重要なのは「分割」の時の考え方です。
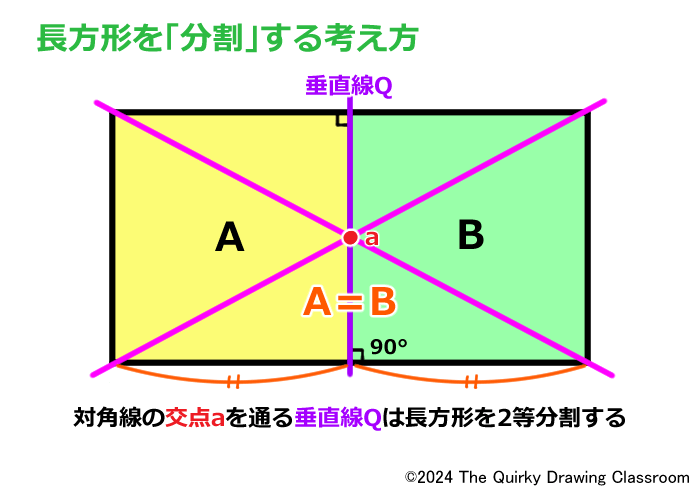
これは長方形を2等分割したものですが、対角線の交点a(中点)を通る垂直線Qを使って長方形を左右に同じ面積のユニットに分けています。
この時、左のユニットAと右のユニットBは同じ大きさに均等分割されています。
ここで右のユニットBを消して左のAだけにしてみると、長方形の面積自体は半分になります。
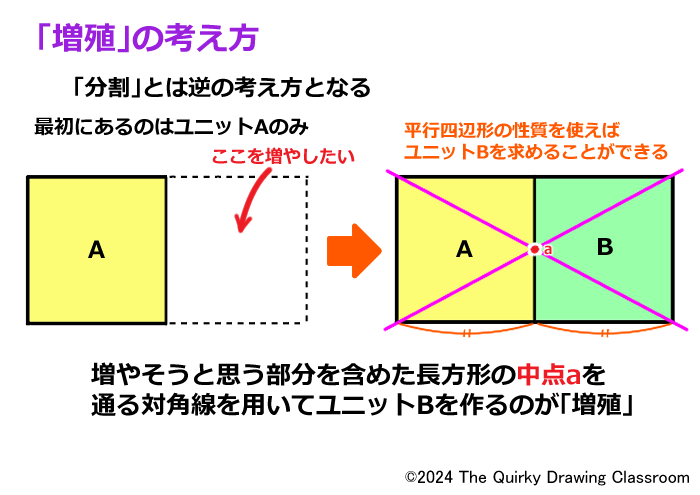
絵を描こうと思った時に与えられたものがユニットのAだけで、あとから右のBを描き加えたと考えるとユニットのAと同じものが右に増えているということになります。
最初のユニットを四角形の半分だけと考えて、対角線とその交点(中点)を使ってユニットを増やしていく…、これが「増殖」の考え方です。
同じユニットを2つに増やす方法
「増殖」の仕組みを2つに増やす考え方から確認してみます。
これも平面図の長方形を使って考えます。
まず最初のユニットとしてAがあり、これを右に増やしたいと思います。
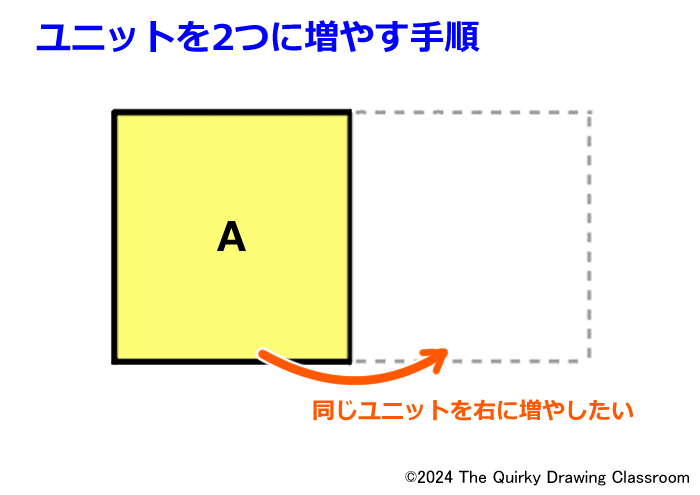
この時、「分割」と逆の考え方をします。
長方形の右側の辺を「分割」の時の垂直線Qと考えます。
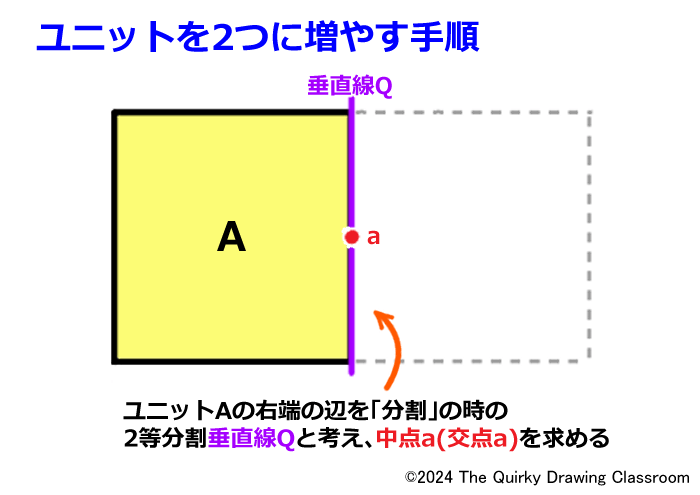
そして、定規などで計って垂直線Qのちょうど真ん中の点(中点a)を求めます。
中点aはユニットAの対角線を用いて求めることもできます。
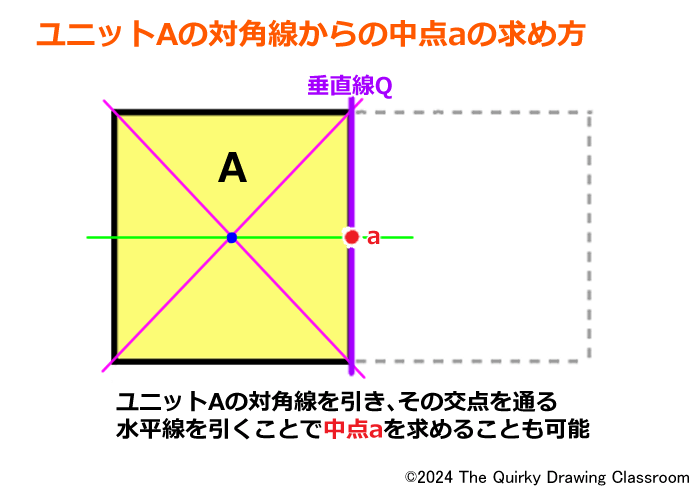
この垂直線Qの中点aは「分割」の時の長方形全体の中点aと同じ点となります。
中点aができたら、ユニットAの左側の辺の上か下の角から中点aを通る直線を引きます。
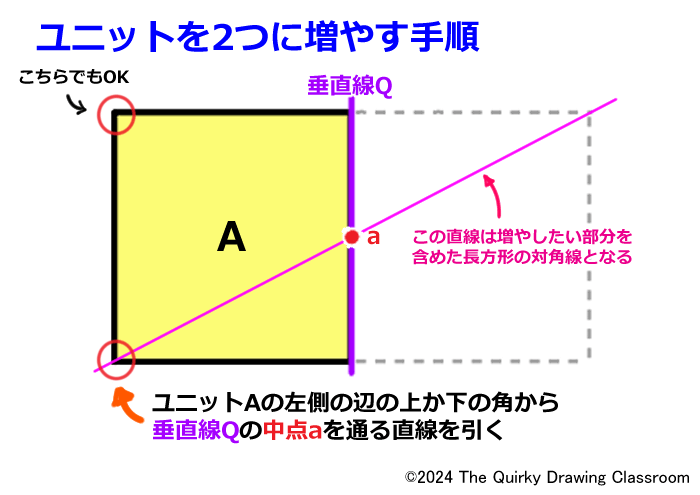
この直線は増やしたいユニットも含めた長方形全体の対角線ともなります。
ここでは下の角からちょっと長めに描いておきます。
交点aを通る直線が描けたら、ユニットAの上の辺を右側に伸ばして交点aを通る直線と結びます。
この点は右側に増やす長方形の右上の角となります。
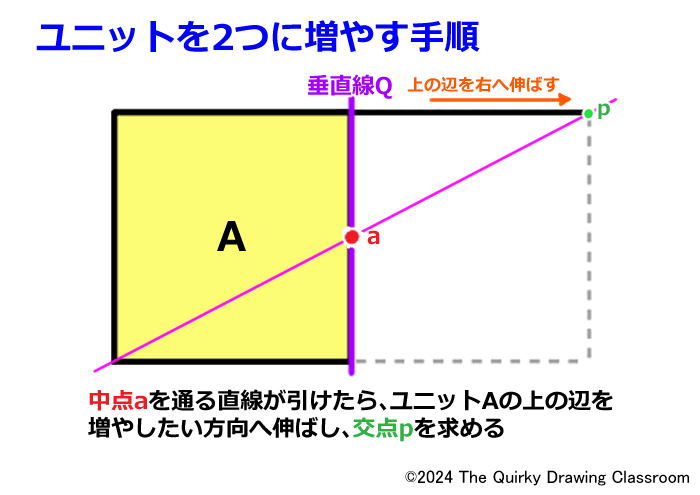
名前を「p」としておきましょう。
交点pが求められたら、そこから下に向けて垂直線を伸ばします。
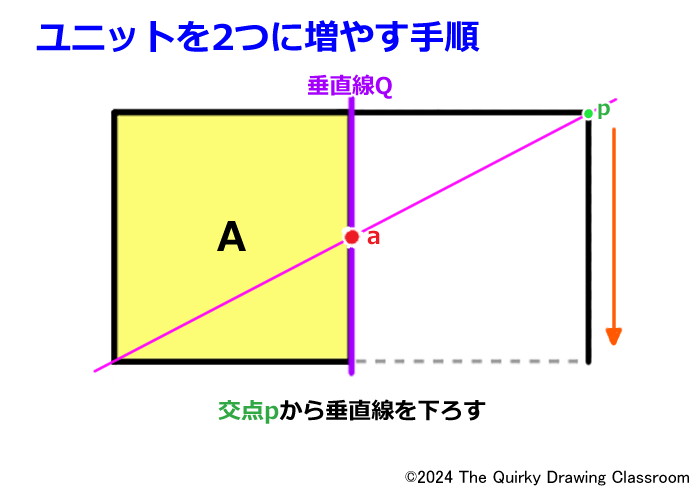
垂直線が引けたら、ユニットAの下の辺も右へと伸ばします。
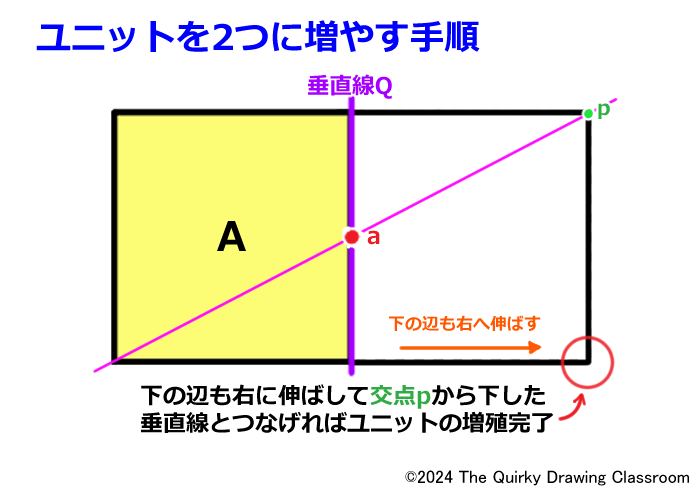
これでユニットAの右隣にAと同じ面積の長方形ができあがります。
この長方形が右に増やすべきユニットBということになります。
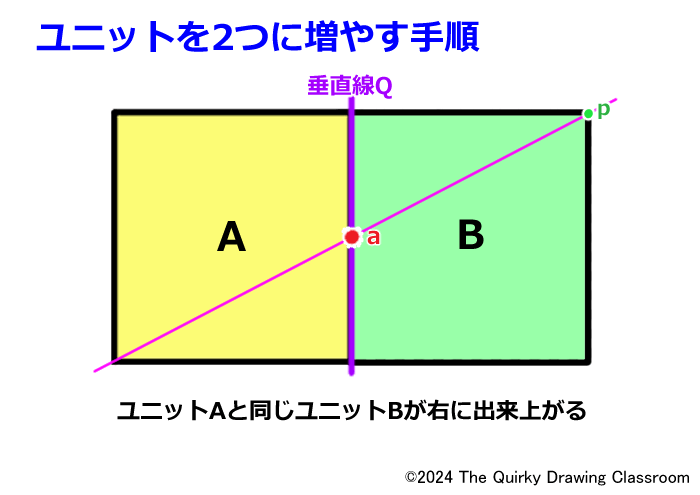
ユニットAが右側に「増殖」され、同じ面積をもつユニットBができあがりました。
これが「増殖」です。
「増殖」では最初のユニットの増やしたい方向側の辺を「分割」の時の均等分割垂直線とみなし、この垂直線を2等分する点を増やしたいユニットを含めた四角形の中点と考えて、そこを通る対角線を使ってユニットを増やしていきます。
これをパースのついたユニットにも当てはめてみましょう。
Aの板をパース上で「増殖」させて、右奥側にユニットBを増やしてみます。
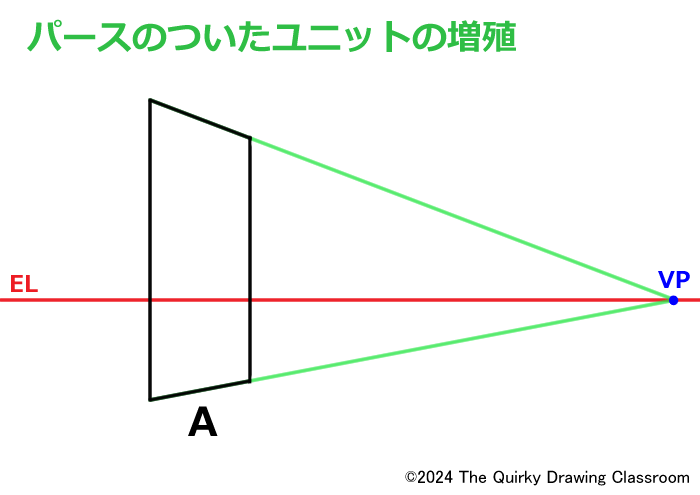
平面図の時と同じように、まず右のBも含めた長方形の中点aの位置を求めます。
定規を使わない中点の求め方は、元のユニットAの対角線を使います。
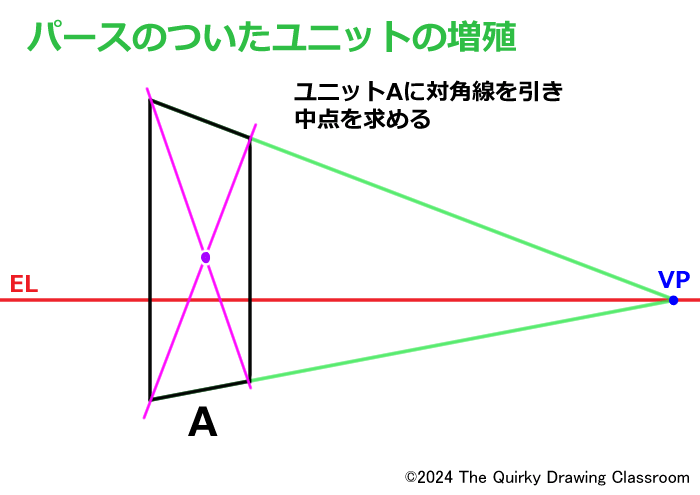
この対角線の交点はユニットAの中点になりますが、この中点を通って消失点に向かうパース線はAを上下に2等分する線でもあります。
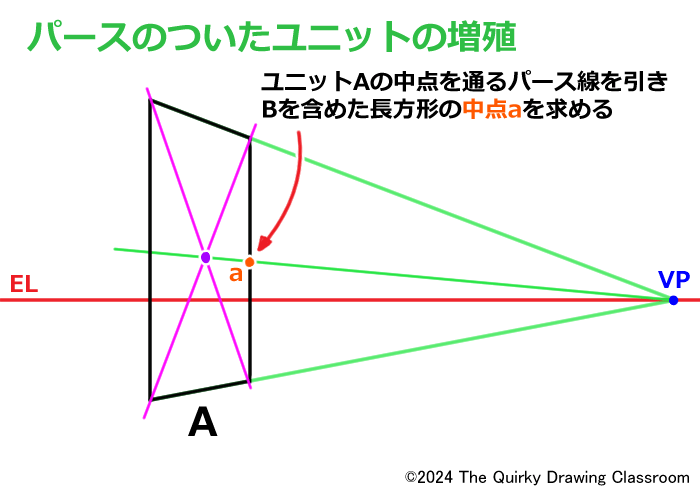
ユニットAの奥側(右側)の縦の辺とこのパース線の交点も縦の辺を2等分する点となります。
そして、ここが求めるべき右のBも含めた長方形の中点aとなります。
中点aが求められたら、ユニットAの手前となる辺の上下どちらかの角から中点aを通る直線を引きます。
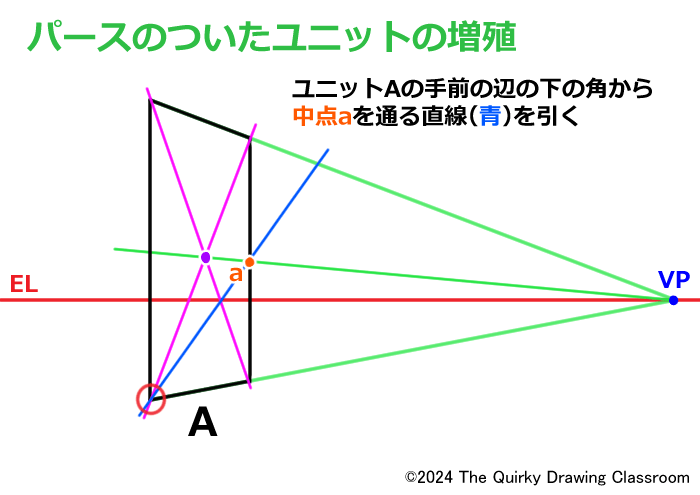
この直線は右のBも含めた長方形の対角線となるものです。
対角線となる直線が描けたら、ユニットAの上の辺を右奥へと伸ばしていきます。
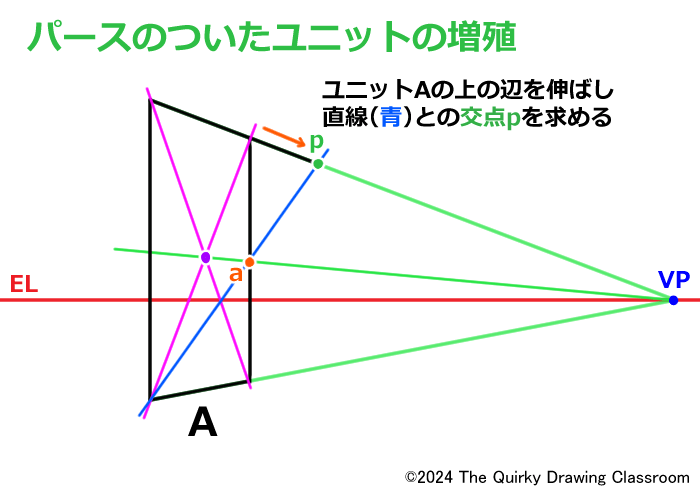
すると対角線となる直線と交わる点が出てくると思います。
ここが交点pです。
交点pが求められたら、そこから垂直線をおろします。
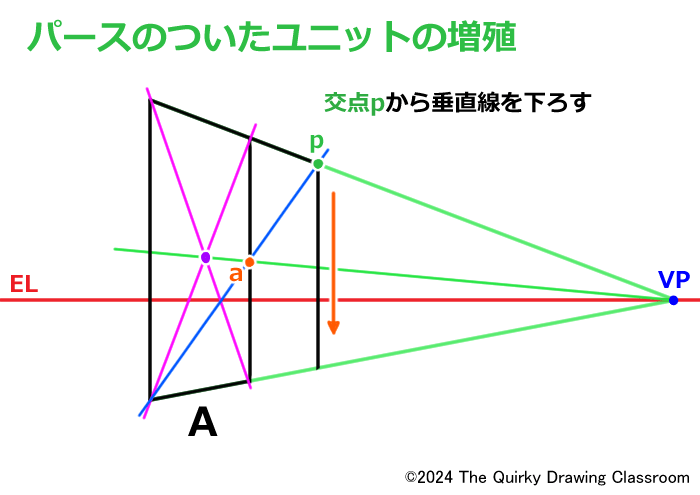
さらにユニットAの下の辺を伸ばして、垂直線と結んだら、ユニットAと同じ面積を持つユニットBがパース上に完成します。
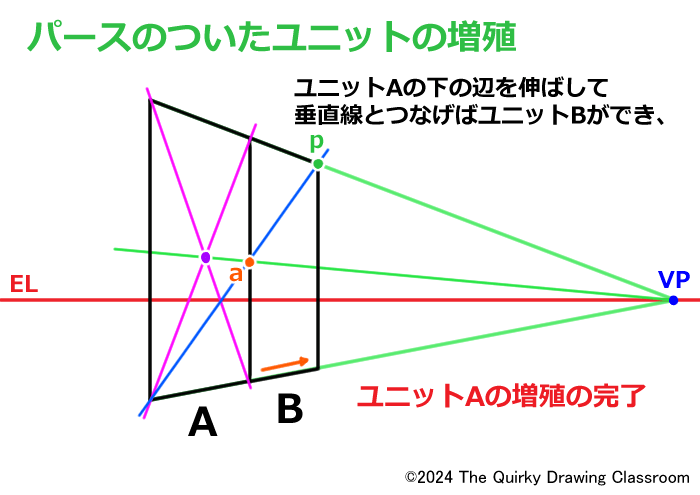
以上が「増殖」の知識を使ってユニットを2つに増やす方法です。
パースがついても考え方自体は平面図の時と同じです。
「増殖」では、この手順がすべての基本となります。
同じユニットを3つに増やす方法
次に3つに増やす方法についても説明しておきます。
「分割」の時は、2等分割する時と3等分割する時の理屈にはかなりの違いがありましたが、「増殖」は2つに増やす時も3つに増やす時も考え方は基本的に同じです。
2つに増やす方法を知っていれば、3つに増やすのはとても簡単です。
例として先ほど2つに増やしたユニットBの右隣に、さらにユニットCを足してみましょう。
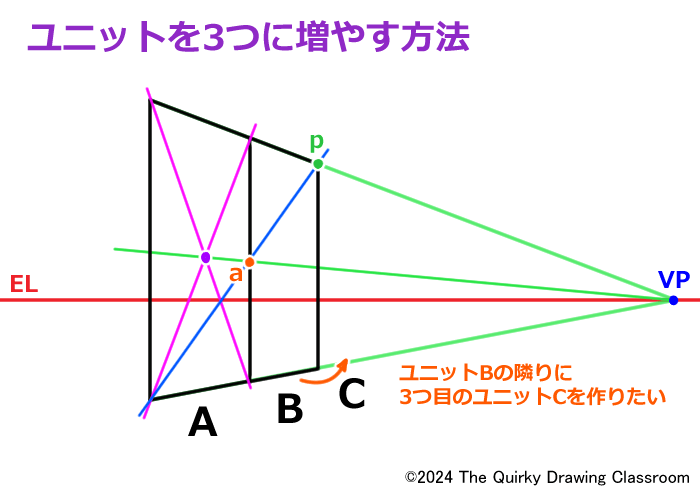
手順はユニットBを増やした時と同じです。
今度はユニットBを基準としてユニットCを増やします。
先ほどと同じようにBの右側の辺の中点を取ります。
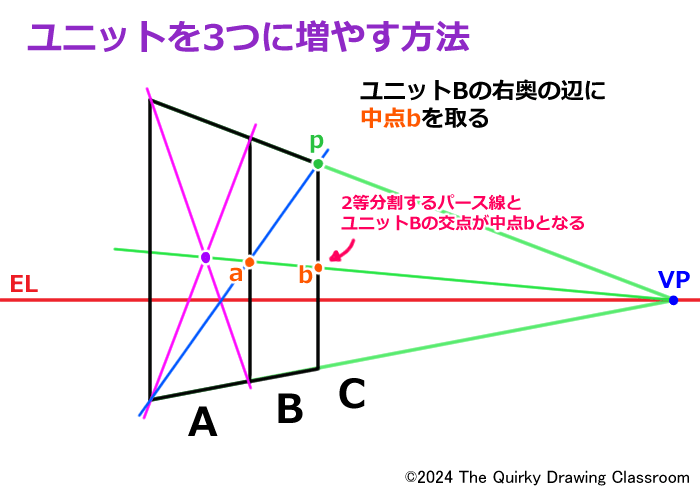
ここをCを含んだ長方形の中点bとします。
中点bが決まったらBの右下の角からbを通る直線を伸ばします。
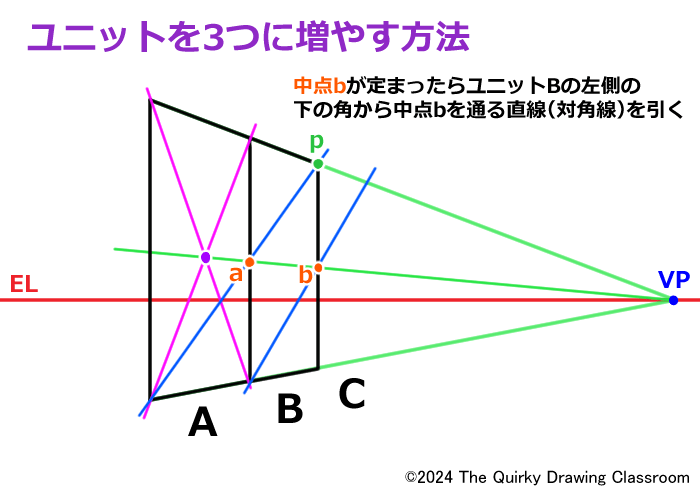
これはユニットBとCで構成する長方形の対角線でもあります。
対角線を引いたらBの上の辺を伸ばして、対角線との交点qを求めます。
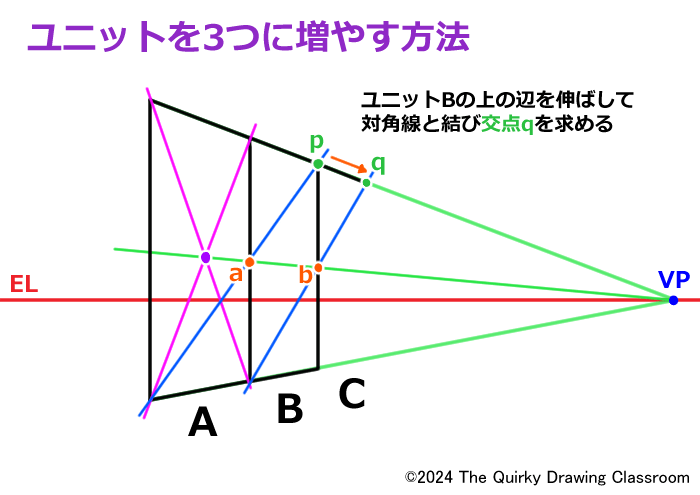
qから垂直線をおろし、Bの下の辺を伸ばしたものとつなげればユニットCの完成です。
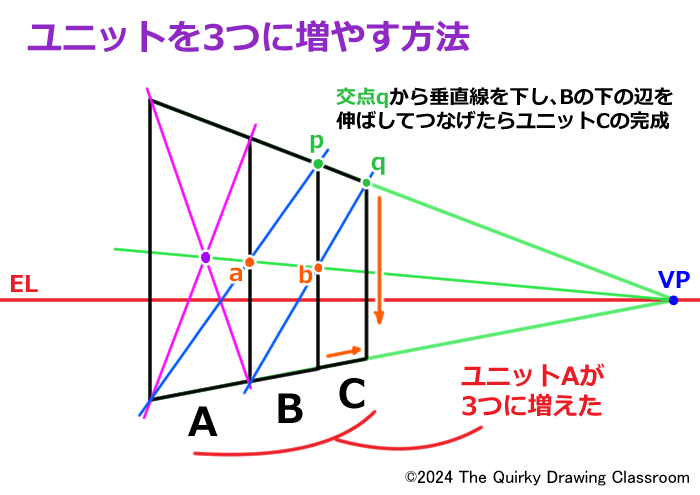
これで最初のユニットAが3つに増えました。
このあと、ユニットを4つ、5つ…と増やしていく時も手順は同じです。
増やす側の辺を2等分する点を求め、そこを中点とする四角形(平行四辺形)の対角線を使って増やすユニットの位置を割り出して「増殖」させてくという手順です。
「増殖」は、これを繰り返していくだけです。
とても簡単です。
実用例:増殖をつかって板塀を描く方法
最後に実用的な例題として同じ板で作られた板塀を「増殖」を使って描いてみましょう。
庭のフェンスを作ると考えて、こちらの板を最初のものを含んで5枚に増やしてみて下さい。
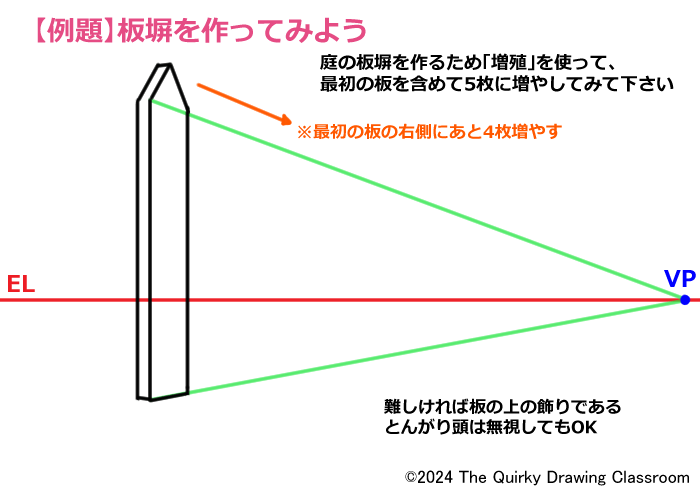
板の先端に簡単な装飾(とんがり頭)がついていますので、こちらもどう描けば良いのか考えてみて下さい。
とんがり頭の先端を正しく板の中心に合わせる場合は「分割」で考えるとよいでしょう。
例題の答えは、この記事の最後に載せておきます。
▼例題の印刷用PDFデータはこちらのリンクからダウンロードできます
▼パースの学習におすすめの参考書はこちらから▼
要点まとめ
では、今回の要点まとめです。
「増殖」は「分割」に比べると考え方は簡単です。
ユニットを2つに増やす方法を知っていれば、いくつでも増やしていくことができます。
簡単に必要なユニットを増やせる「増殖」、ぜひ知っておいて下さい。
次回は「分割&増殖」の実践編として練習問題を用意します。
パースの知識を習得するためには実際に使ってみることが一番大切です。
より実践的な例題を通して「分割&増殖」の活用に慣れてみましょう。
それでは、また次回。
【広告】▼「基礎から応用まで」パースの勉強におすすめの一冊▼
アメリカの画家ルーミスの名著『初めてのイラスト教室』の再編集復刊版。
ルーミス自身の説明図に加え、復刊にあたりより詳しい日本語版の解説図が追加されています。パースの基礎から応用まで幅広く学ぶことができるおすすめの1冊です。
例題の答え
では、例題の答えです。
まずは最初の板を2つに増やします。
やり方は記事内で紹介した手順と同じです。
板の中点を求めて、VPとパース線で結びます。
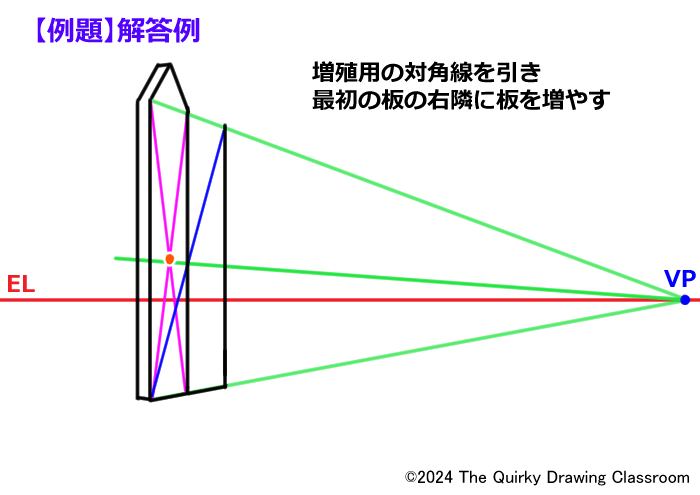
これから描く4枚の板の中点はすべてこのパース線上に来ます。
パース線と右端の辺の交点を通る対角線を引き、右隣にユニットを増やします。
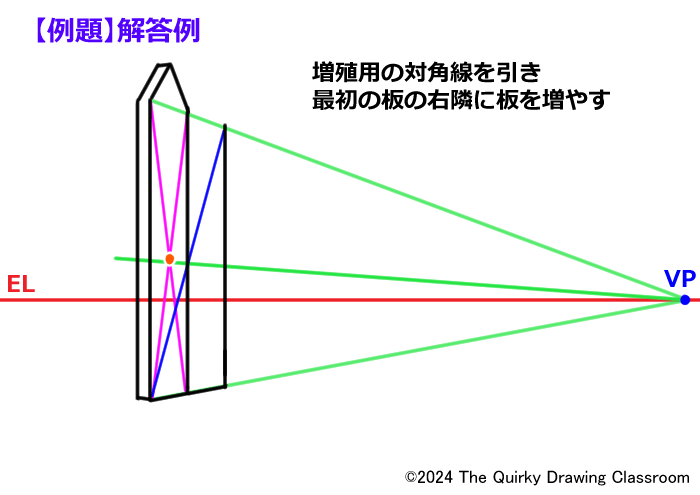
あとはこれを3回くり返すだけです。
これで板自体は5枚に増やすことができました。
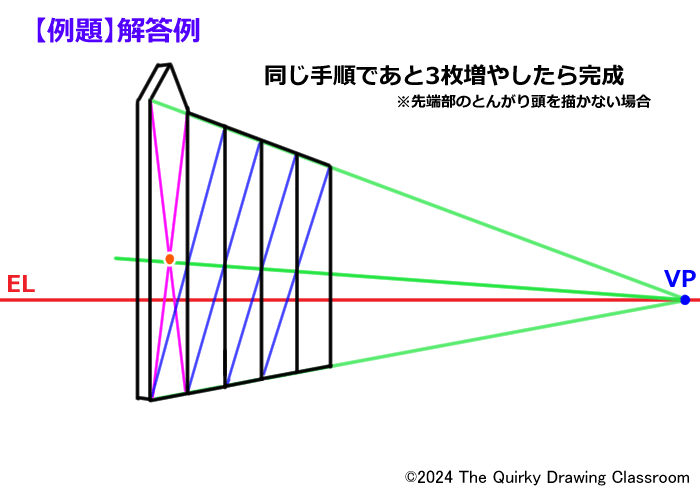
この板には装飾(とんがり頭)が付いていますので、これの描き方も解説していきます。
デッサン的におかしくなければ、フリーハンドで描いてしまってもよいのですが、正確に描く方法も説明しておきます。
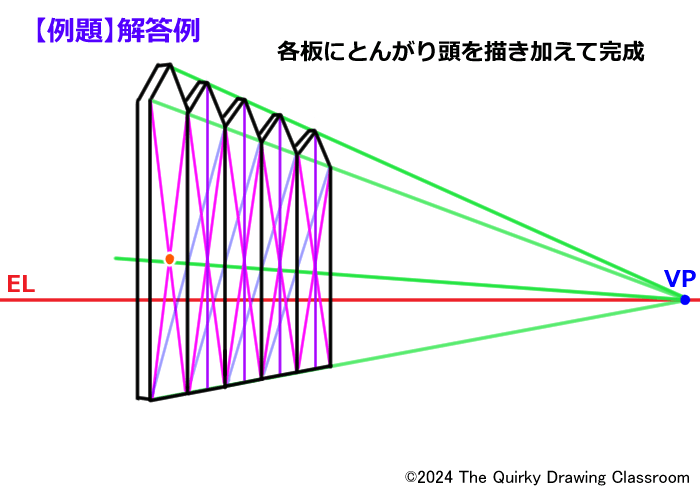
まず、とんがり頭の先端の高さは基準となる板の頭の位置とVPをパース線を引いて求めます。
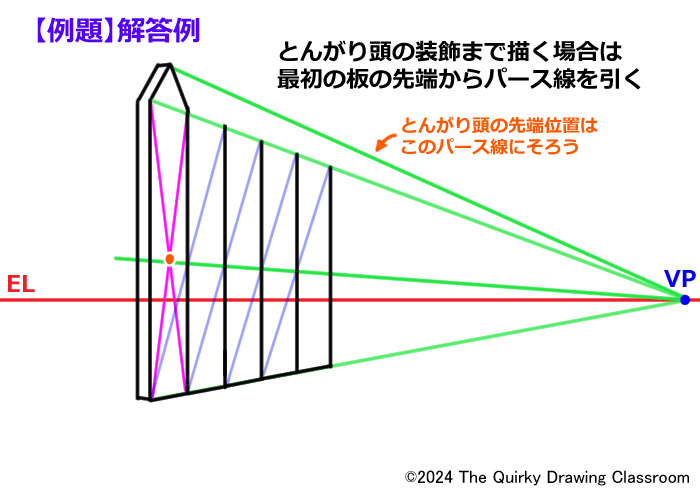
他の4枚の板のとんがり頭の先端は、すべてパース線上にそろいます。
板における横位置は「分割」の知識を使います。
増やした板に対角線を引きましょう。
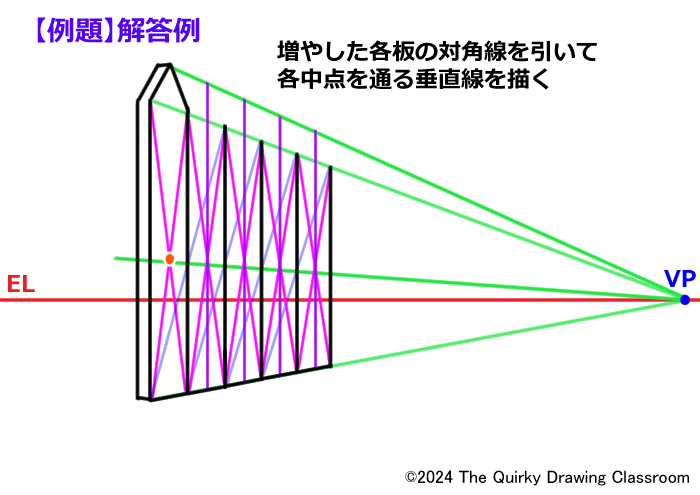
この対角線の交点を通る垂直線は四角形を縦に2等分する直線です。
この直線ととんがり頭の先端位置を示すパース線が交差する点がとんがり頭の位置です。
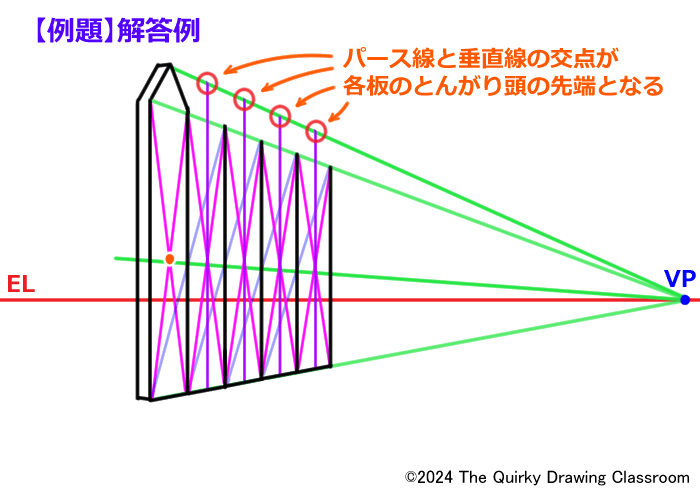
これで先端にとんがった装飾のついた5枚の板がならんだ板塀の完成です。
▼今回の記事が少しでも勉強になったようでしたらクリックしておいて下さい!
にほんブログ村