《初級者~中級者向け》
今回は「分割」と言われる知識の基礎編です。
遠近法における「分割」とは、簡単に言うと「パースのついたユニットを複数に分ける」ことを指します。
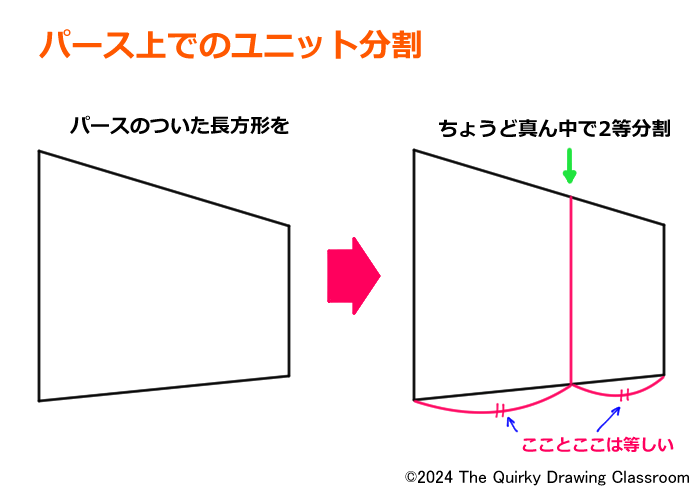
「分割」の中でも、今回は一番簡単な「ユニットの2等分割」について解説します。
この2等分割が「分割」の基礎となります。
次回の「分割応用編」と合わせると、パースのユニット分割を使って、このような複数のユニットに均等分割された板塀やブロック塀などが簡単に描けるようになるでしょう。
「分割」は絵を描く上で非常に便利で、使う頻度も多い知識です。
次回の応用編と合わせて、ぜひ読んでみて下さい。
▼前回記事「2点透視での箱の描き方」はこちら
※本ブログの記事には広告が表示されます。
今回の授業内容と難易度
では、今回の内容です。
「分割」は「分割と増殖」という言い方で、よく「増殖」という知識とセットで説明されることも多いのですが、先に「分割」のみにしぼって説明します。
「分割」を知っておくことは「増殖」を学ぶ上の基礎となりますし、「増殖」について理解しやすくなると思います。「増殖」については改めて解説します。
何より説明もしやすいですので。
今回は「分割」の基礎編という位置づけです。
パース上にある板を2つに分割できるところを目指します。
- 難易度 1:★☆☆☆☆
- 重要度 4:★★★★☆
- 画力向上度 2:★★☆☆☆
基礎編で難易度は低いですが、重要度は高いです。
「分割」においては、まず「ユニットを2つに分ける方法」を理解することが基礎となるからです。
2等分割する方法は知ってしまえば、とても簡単な知識です。
どういう時に「分割」を使うのか?
では、具体的にどんな時に「分割」を使うのでしょうか?
真ん中はどこ?
最初に簡単な練習問題をやってみましょう。
こちらに2点透視で描いた板を立てた絵があります。
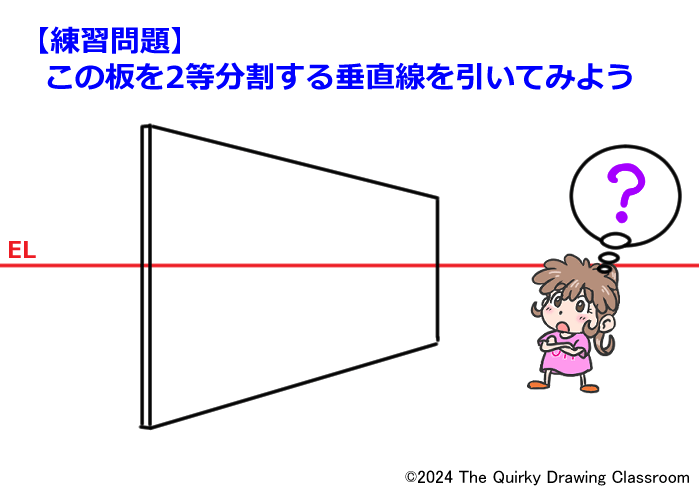
こちらの板をちょうど板の真ん中を通る垂直な直線で2つに等しく分けるためにはどうすればよいでしょうか?
A、B、Cの3つのパターンを描いてみました。
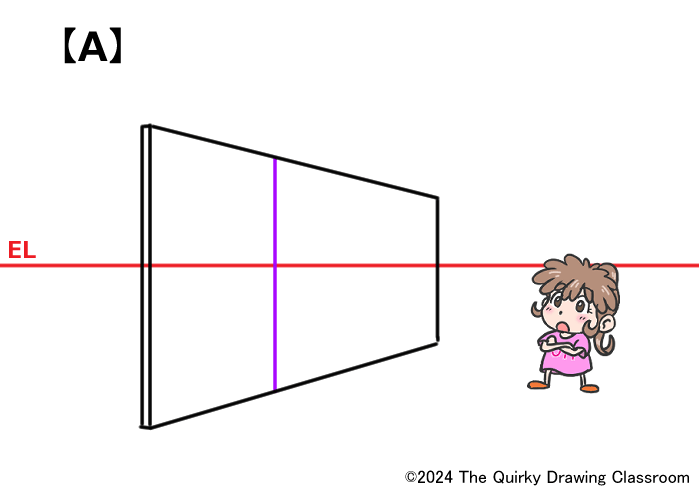
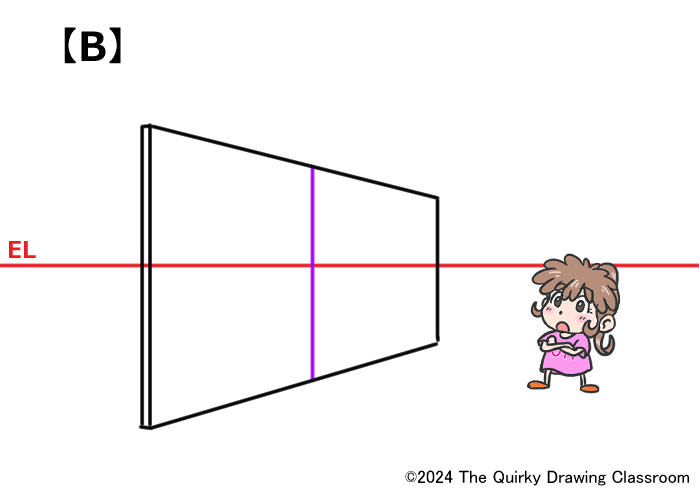
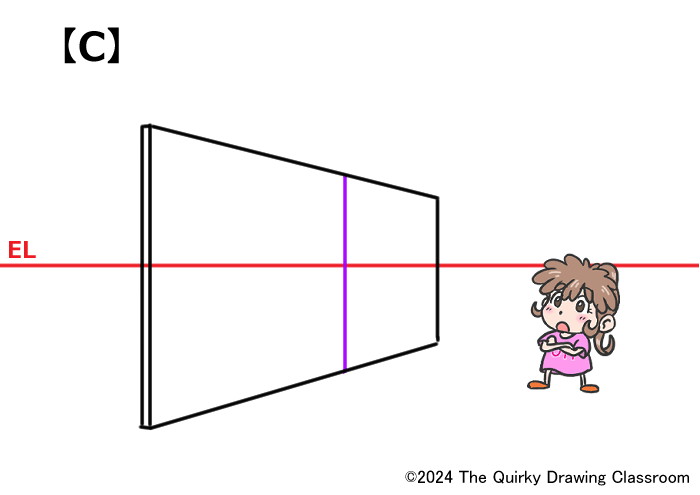
このパースのついた奥行きのある板をちょうど真ん中で2等分する線の位置として、正しいと思われるものをA、B、Cの中からひとつ選んでみて下さい。
【答え】
どうでしょうか?
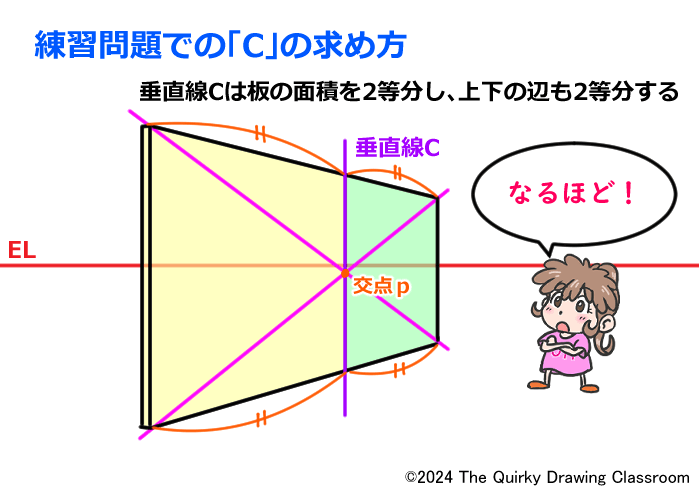
この問題の答えは「C」です。
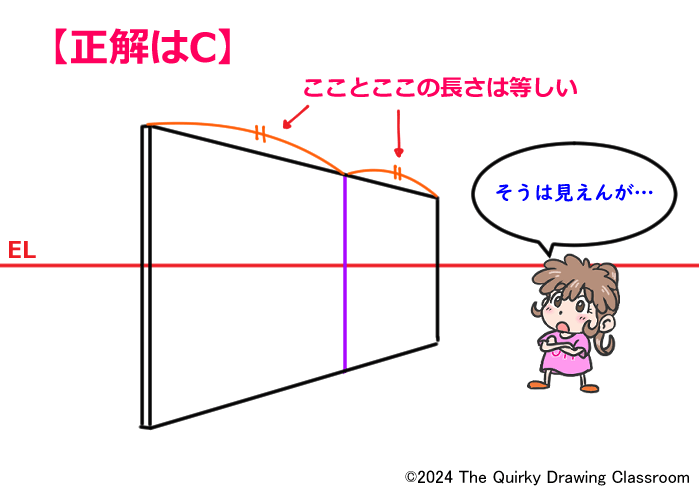
パッと見た印象だけだと「B」が正しいように見えますが、正解は「C」になるのです。
ユニットを等しく分ける「分割」
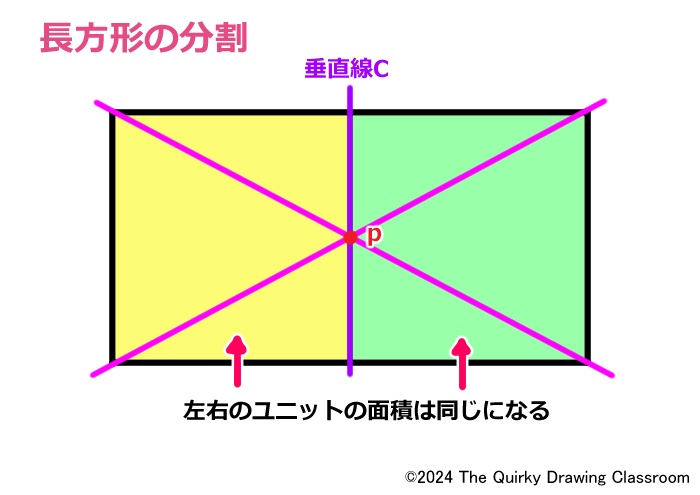
この練習問題で正解とした「C」の垂直線は、「分割」を使って求めています。
「分割」の基礎であるユニットの2等分割を知っていれば、このCの垂直線が求められます。
簡単に説明すると、今回の板(パースのついた長方形)に対角線を引き、その交点を通る垂直な直線がCであり、この垂直線Cは板の面積を2等分する線で、上下の各辺も2等分しています。
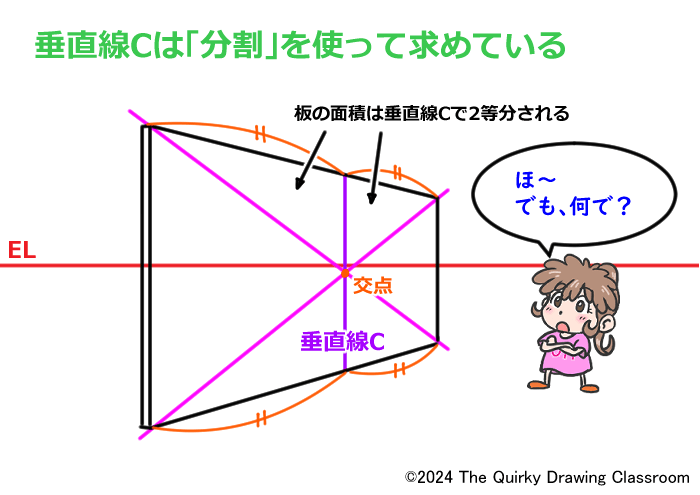
以下で、なぜこの垂直線がユニットを2等分割していると言えるのかを確認していきます。
パース分割の考え方
パースに関する知識はパースがついたまま考えると難しくなってしまいます。
なので、今回の板も平面的な長方形(平行四辺形の一種)として考えてみましょう。
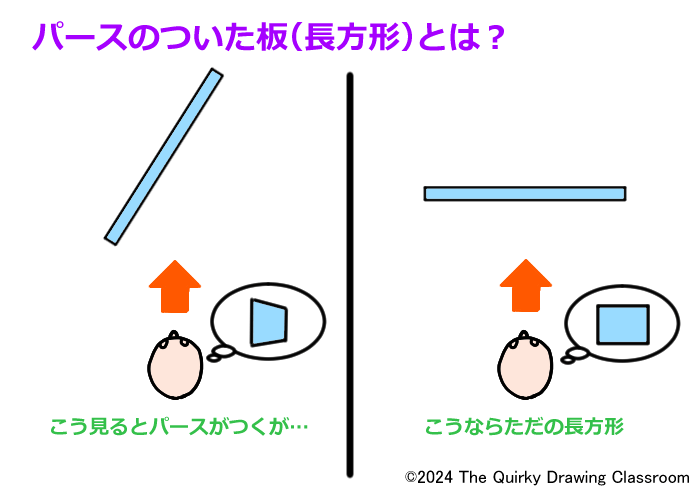
今回のパースのついた板も、単に長方形を見る角度が変わっただけです。
長方形として持っている性質は、パースが付いても変わることはありません。
長方形が持つ性質
そして、ここで長方形(平行四辺形)が持つ性質を確認しておきましょう。
おそらく中学校くらいで習うかと思いますが、「平行四辺形の対角線の交点を通る直線はその四角形の面積を2等分する」という性質です。
長方形や正方形も平行四辺形なので、当然この性質が当てはまります。
長方形を2等分割する方法
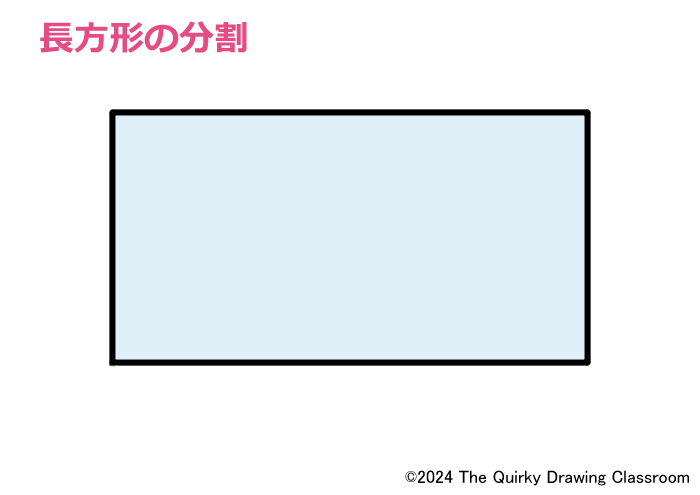
では、平面図となった長方形を2等分割してみます。
まず最初に平面の長方形の対角線を引きます。
対角線が引けたら、その交点には「p」と名前を付けておきます。
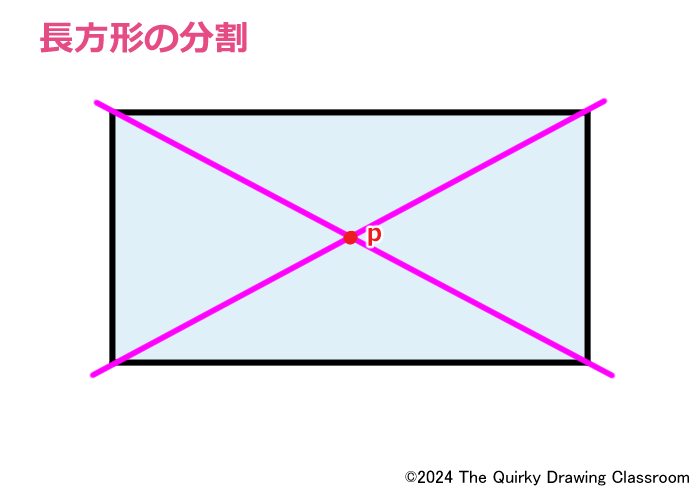
長方形の持つ性質から言えば、この「p」を通ればどのような直線でもこの板を2等分割できるのですが、今回の練習問題では垂直線で2等分割するとなっています。
先ほどと同じように垂直線Cを描いてみましょう。
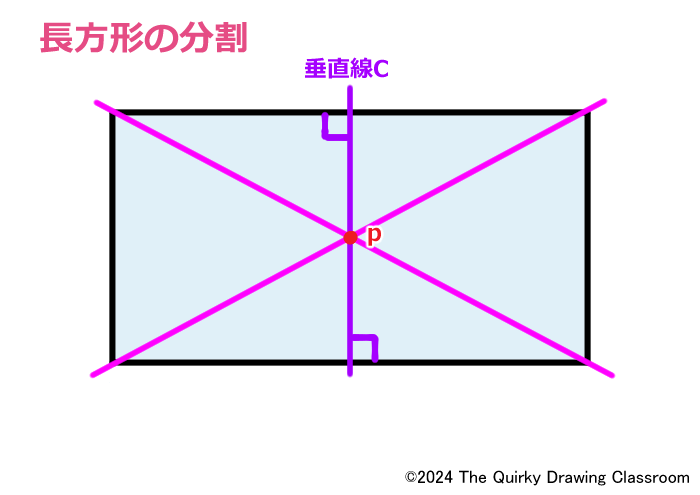
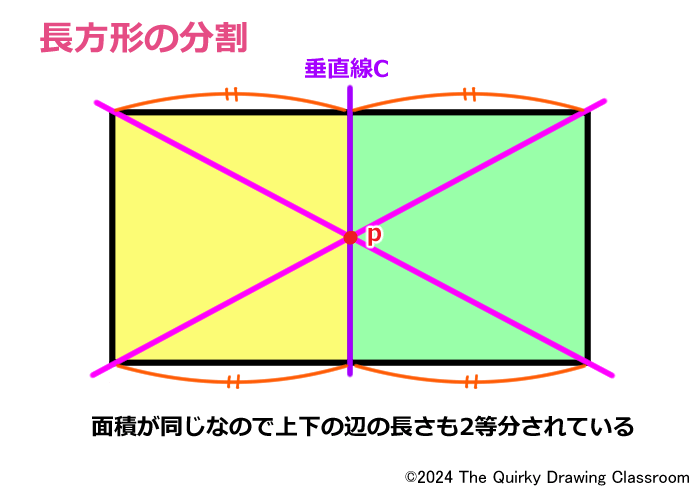
この垂直線Cは、長方形の上辺と下辺に対して垂直に交わる直線です。
長方形の性質にしたがい、垂直線Cは対角線の交点を通る直線ですので、当然この長方形の面積を2等分する線と言うことになります。
面積が2等分されるので上辺と下辺も同じく2等分されていることになります。
2等分割の確認方法
この性質が本当に合ってるかどうかを実際に確認したい場合は、なんでも良いので正方形か長方形の紙を用意してみましょう。
コピー用紙やいらないチラシなどが手近でよいでしょう。
この紙に対角線を引いて、中点を通る垂直線を描いてみましょう。
そして、この垂直線にそって紙を折ってみるとぴったりと左右同じ面積で紙が折れると思います。
このことからも対角線の中点を通る直線は長方形(正方形)を2等分割していることがわかります。
パース上での2等分割
長方形(平行四辺形)を2つに等しく分割する方法は、これでわかりました。
それでは、最初のパースのついた板で再度2等分割について考えてみましょう。
パースがつくと難しく思えますが、平面図の長方形と性質は同じです。
長方形で検証した内容をそのまま当てはめればOKです。
パースのついた板の2等分割
パースがついている場合も、まず対角線を引きます。
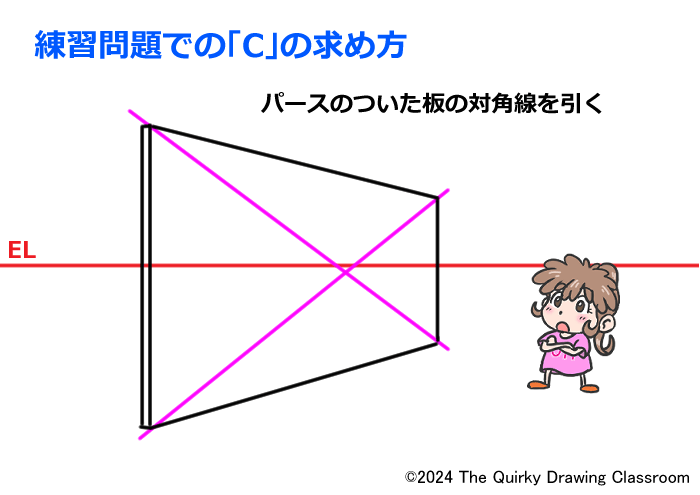
このような感じです。
対角線が引けると交点pができますので、ここを通る垂直線Cを描きます。
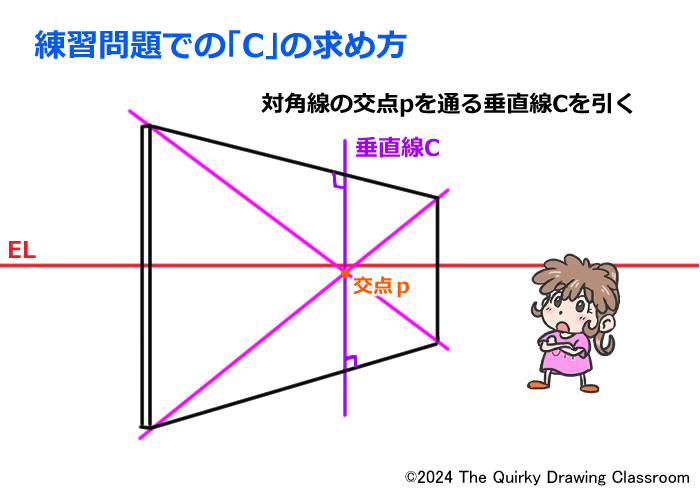
これだけです。
これで最初の板は2つに等しく分割されたことになります。
2等分割の実用例
では、このパースの2等分割をどのように使うかも考えてみましょう。
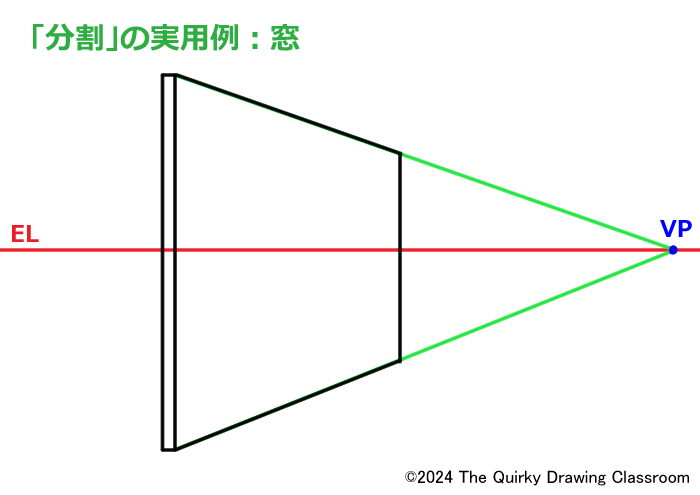
これは一例ですが、例えば窓です。
住宅などにある窓は同じサイズのサッシが左右にならぶ場合がほとんどです。
この窓にパースがついている場合に、この2等分割を使います。
まず住宅の壁となる四角形をパース上に描きます。
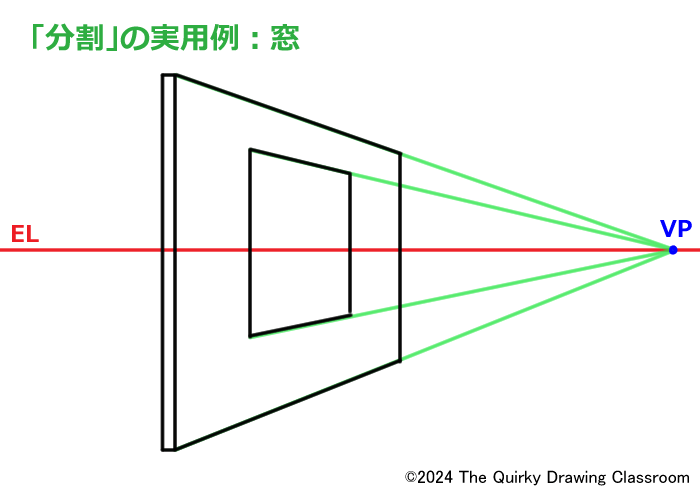
さらに窓となる四角形を描き加えます。
この窓の四角形を対角線で2等分割して、細部を描きこめば窓の完成です。
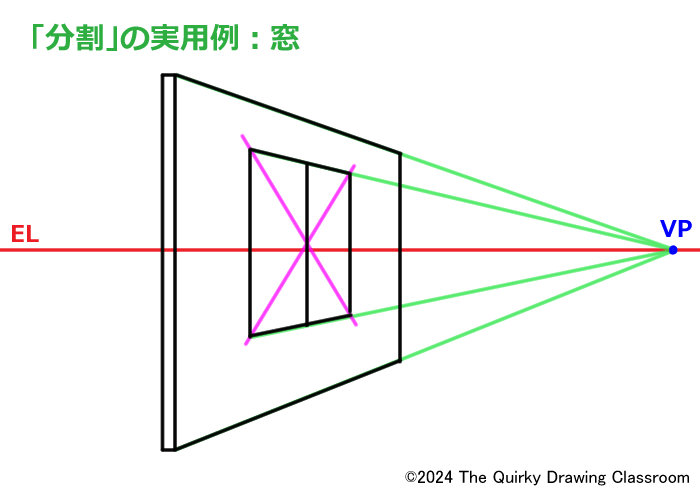
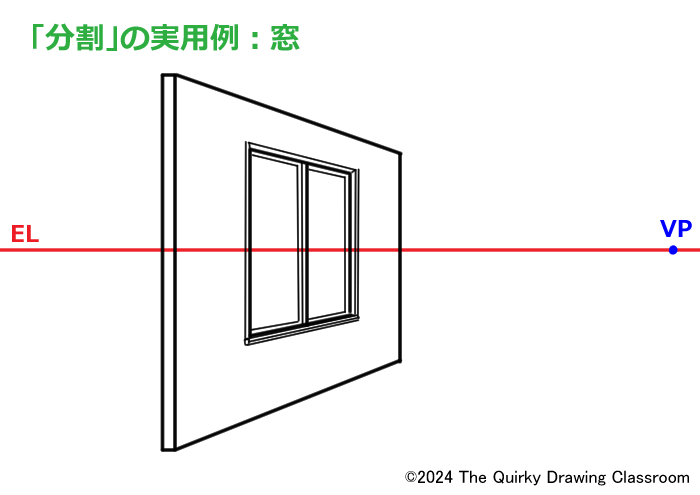
もし、壁の真ん中に窓を設置したいのであれば壁を2等分割すれば窓の位置がわかります。
この場合、壁を2等分割する垂直線と窓のサッシの真ん中の線は同じになります。
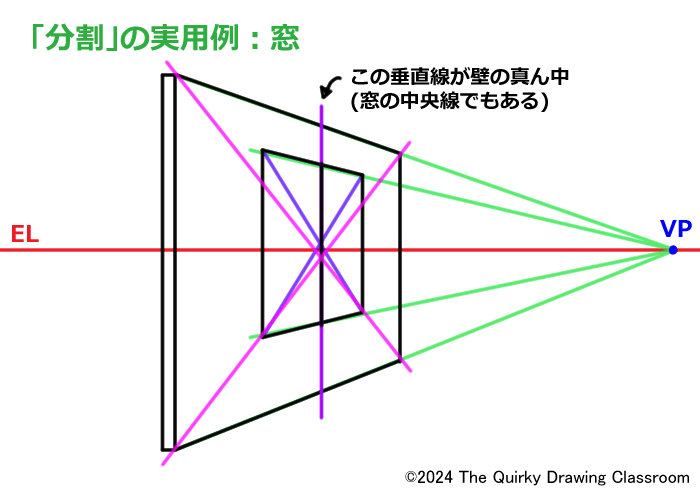
窓はあくまで一例ですが、ユニットを2等分割する方法を知るだけでも色々なものを正確に2つに分割して描けるようになります。
「分割」の基礎として、ぜひおぼえておいて下さい。
▼パースの学習におすすめの参考書はこちらから▼
要点まとめ
では、要点まとめです。
「パースの分割」は知っていると色々なところで使える便利な知識です。
まずは「なぜ2つに等しく分割できるのか」という基本的な理屈を知っておきましょう。
2等分割の理屈がわかればより複雑な分割についても理解しやすいでしょう。
次回は「分割」の応用編です。
より実用的な「分割」の使い方と、簡単な分割の方法について解説します。
それでは、また次回。
【広告】▼「基礎から応用まで」パースの勉強におすすめの一冊▼
アメリカの画家ルーミスの名著『初めてのイラスト教室』の再編集復刊版。
ルーミス自身の説明図に加え、復刊にあたりより詳しい日本語版の解説図が追加されています。パースの基礎から応用まで幅広く学ぶことができるおすすめの1冊です。
▼今回の記事が少しでも勉強になったようでしたらクリックしておいて下さい!
にほんブログ村