《初級者~中級者向け》
今回は「分割」の応用編です。
ユニットの3等分割を主に、3つ以上に均等分割する方法を説明します。
前回の基礎編でパース上のユニットを2等分割する方法を解説しています。
今回の内容は、この2等分割が基礎となりますので「分割についてよくわからない…」という人は、こちらの記事を先に読んでもらった方が理解がしやすいと思います。
▼前回記事:「分割の基礎編」はこちら
今回の応用編ではユニットの3等分割からはじめて、それ以上のユニットに分割する方法について説明していきます。
記事の最後では、とても簡単にユニット分割する方法についても説明します。
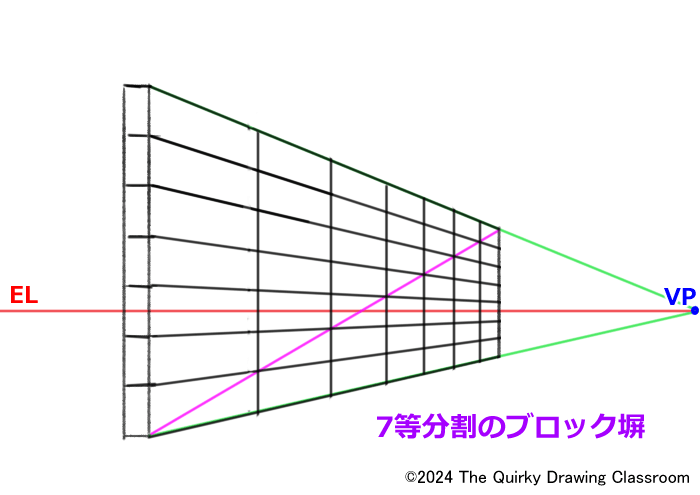
最終的にはこのようなブロック塀が簡単に描けるようになるようになるでしょう。
※本ブログの記事には広告が表示されます。
今回の授業内容と難易度
では、今回の内容です。
まず、ユニットを3等分割する理屈と方法について説明します。
その上で3つ以上に均等分割する方法についても説明します。
2等分割は「分割」の基礎ですが、それで描けるものは限定的です。
実際に色々な絵を描くためには3等分割以上の分割方法を知っておくほうが実践的です。
- 難易度 3:★★★☆☆
- 重要度 4:★★★★☆
- 画力向上度 3:★★★☆☆
3等分割は2等分割に比べるとちょっと難しくなります。
しかし「どうすれば3つに分割できるのか?」という考え方や分割の道筋については、しっかり整理して理解しておく必要があるでしょう。
3等分割の理屈は少しややこしいのですが、別のやり方でとても簡単に複数のユニットに分割することも可能なので、それについても説明します。
ただ、「なぜそうなるのか?」の理屈を知っておいた方が分割についての理解が深まると思いますので、3等分割について詳しく説明したあとで、この簡単な方法について説明します。
「理屈は良いからすぐに知りたい!」という人は、こちらから該当項目へ移動して下さい。
3等分割のやり方と考え方
2つに等しく分割する方法は前回記事で解説しました。
今回は、まずユニットを3つに等しく分割する方法について説明をします。
わかりやすいように2等分割の時と同じような板を使って説明します。
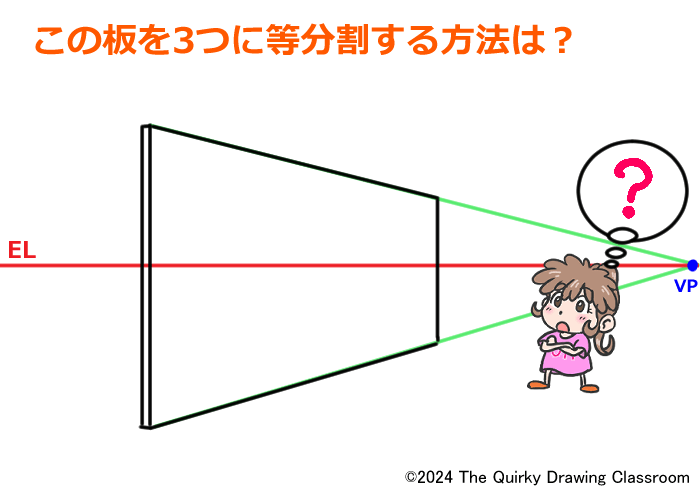
この1枚の板を今度は3つの同じ形のユニットに分割するわけです。
2等分割の時のように長方形の対角線だけを使って分割することはできそうにありません。
一度2分割したユニットに対角線を引いて、さらに分割しても4等分割になるだけです。
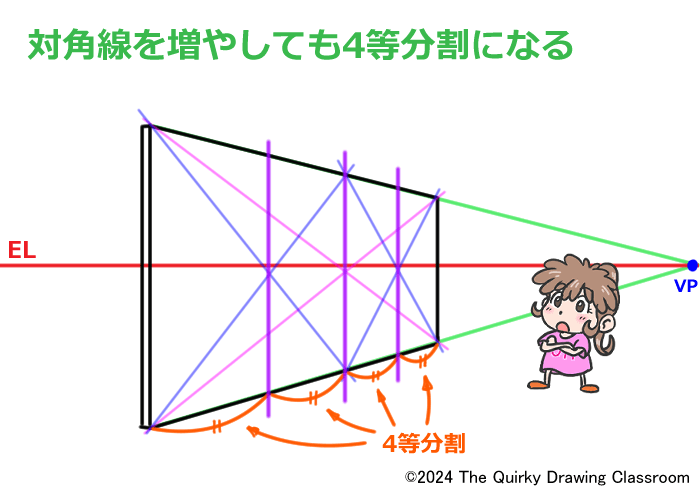
3等分割はちょっと難しそうです。
先に3等分割の答えを描いてみると、このようになります。
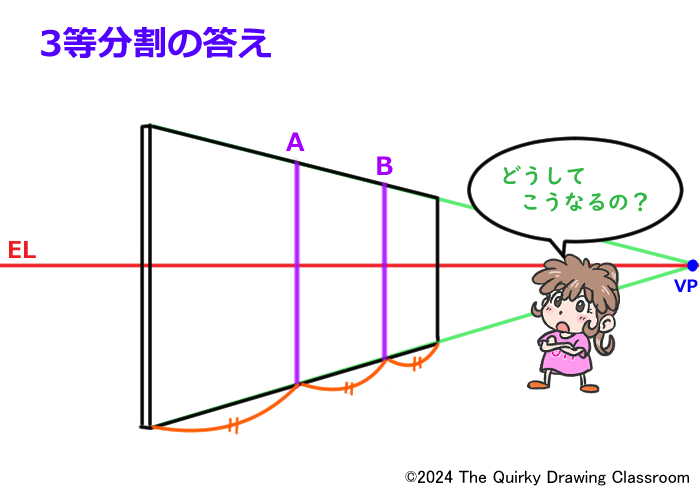
紫で描いた2本の垂直線AとBが、この板を3つのユニットに等しく分割しています。
3等分割となる理由
これでどうして3等分割できるのかは、平面図を使って答えから手順を逆にたどりながら説明します。
サイズも決まっていた方がわかりやすいと思うので、仮に今回の板の高さを3m、横幅を9mとして考えてみます。
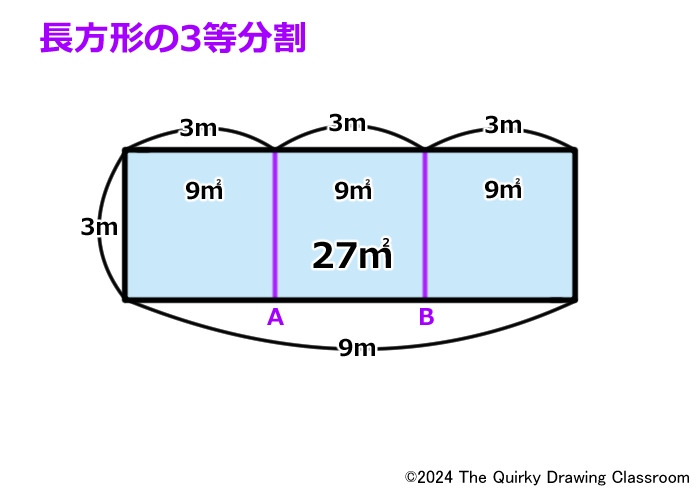
すでに3等分割されている3つのユニットの横幅はそれぞれ3mです。
板全体の面積は、3m×9m=27㎡ です。
これを3等分割するので、分割された各ユニットの面積は、3m×3m=9㎡ となります。
すでに3等分割された元の板となる長方形に対角線を引いてみます。
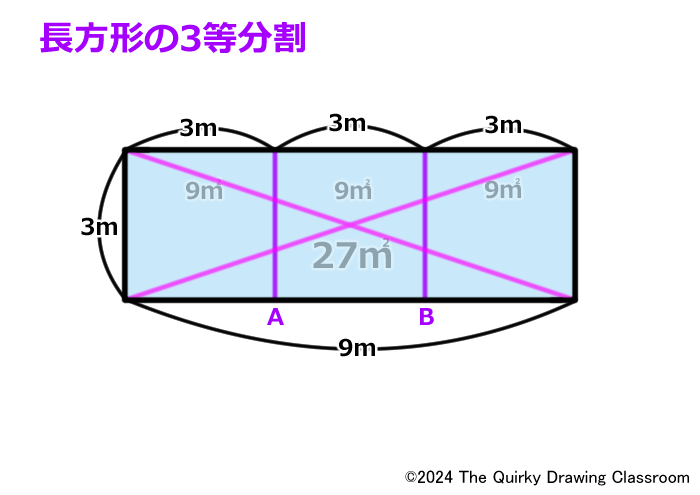
すると板を3等分割する垂直線A、B上に4つの交点ができました。
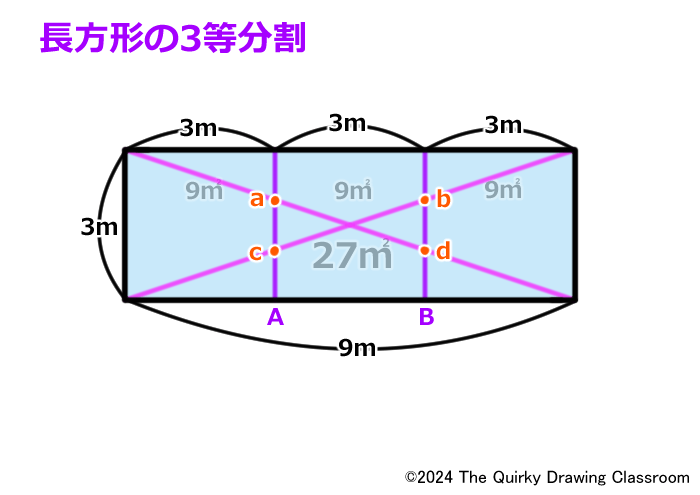
この4つの交点にそれぞれa、b、c、dと名前をつけておきます。
そして、ここで交点aに注目してみましょう。
交点aは、この板の中に隠れた別の長方形の中点となっているのに気づくでしょうか。
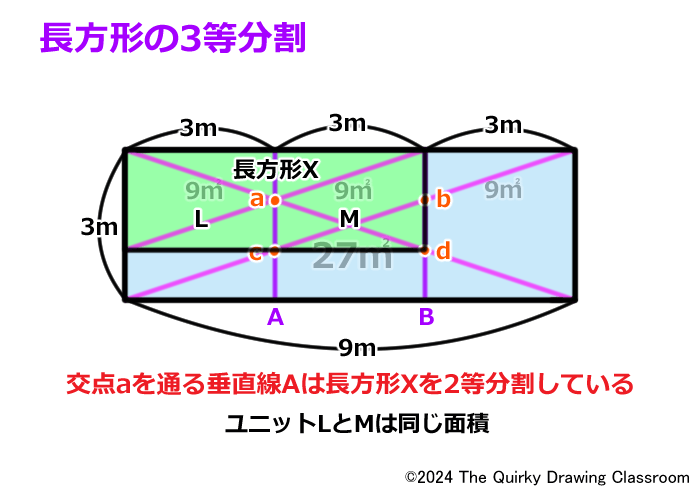
その長方形とは、この長方形です。仮に「X」と名前を付けておきます。
長方形Xの中点となるのは交点aなので、2等分割した時と同じ理屈で長方形Xは垂直線Aで分けられた左右のユニットLとMは等しく2つに分割されていると言えます。
これは長方形の長さが下に伸びたとしても同じです。
そして、今度は交点aの右隣の交点bを見てみましょう。
この交点bも隠れた別の長方形の中点になっています。
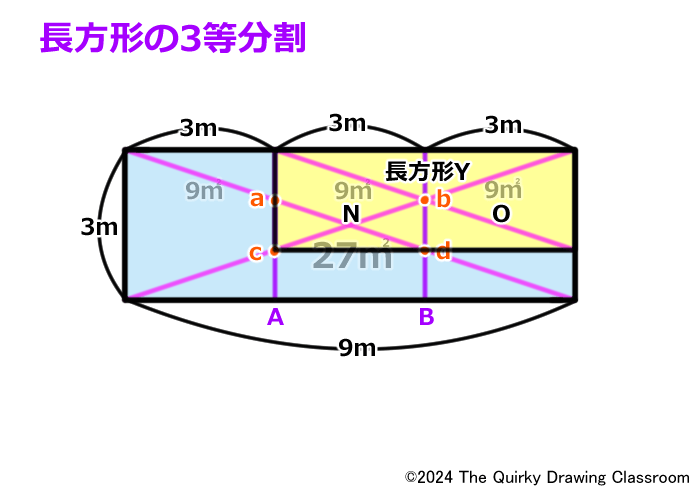
この長方形を「Y」と名付けます。
長方形YはXと真ん中のユニット(M)を共有しています。
このYを見ると、Xと同じように交点bを通る垂直線Bによって左右のユニット(NとO)に2等分割されていることがわかります。
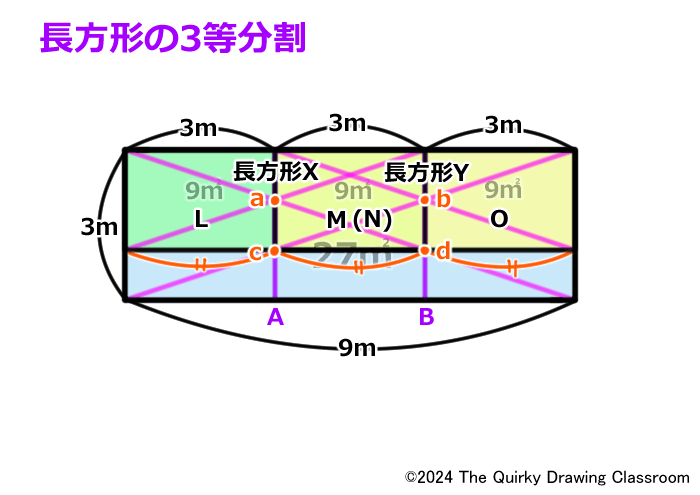
MとNは同じユニットなので、M=Nということなり、L=M(N)=Oで、それぞれのユニットが等しく3つに分割されていることがわかります。
元のパースのついた板にこれを置き換えてみるとこのような感じになります。
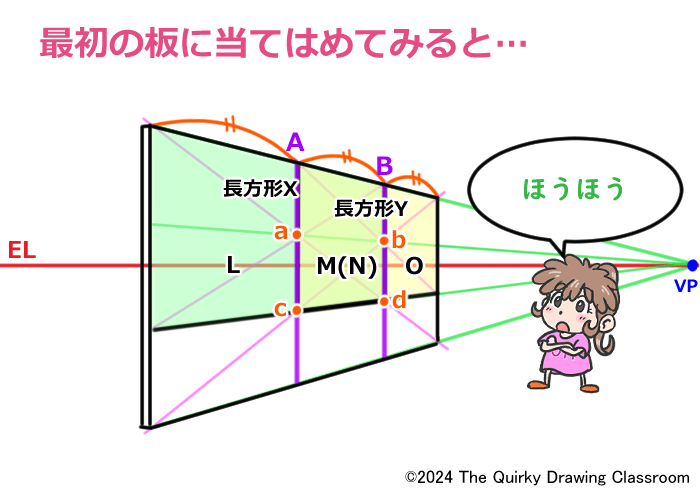
最初に描いた3等分割線である垂直線A、Bに重なります。
3等分割線の求め方
3等分割の理屈の説明が長くなりましたが、では3等分割するために肝心な交点aとbはどのように求めれば良いのでしょうか?
この交点a、bを求めるためには、やはり長方形の対角線を使います。
これもわかりやすいように平面図で考えてみましょう。
長方形に対角線を引き、長方形を2等分割する垂直線を求めます。
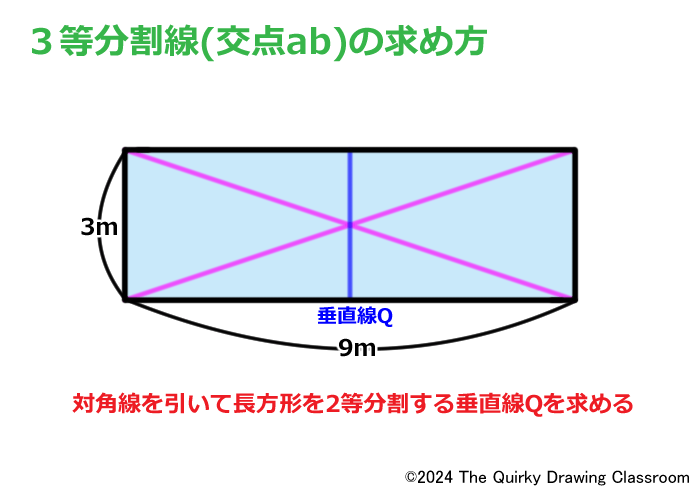
この垂直線は「Q」としておきます。
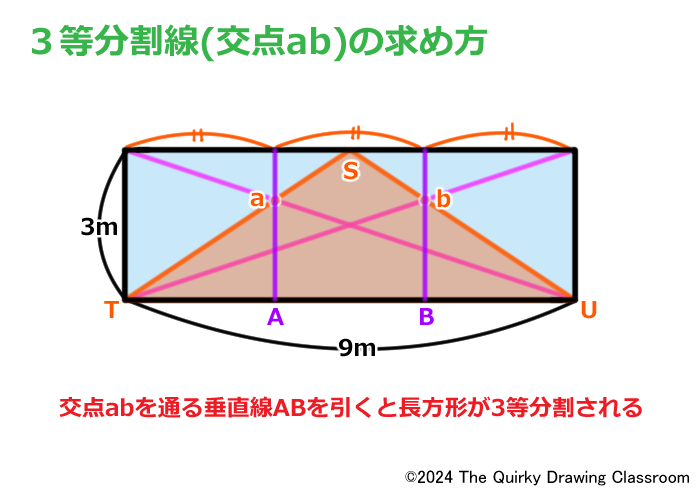
垂直線Qが描けたら、その頂点をSとして、そこから長方形の下の角T、Uに直線を引きます。
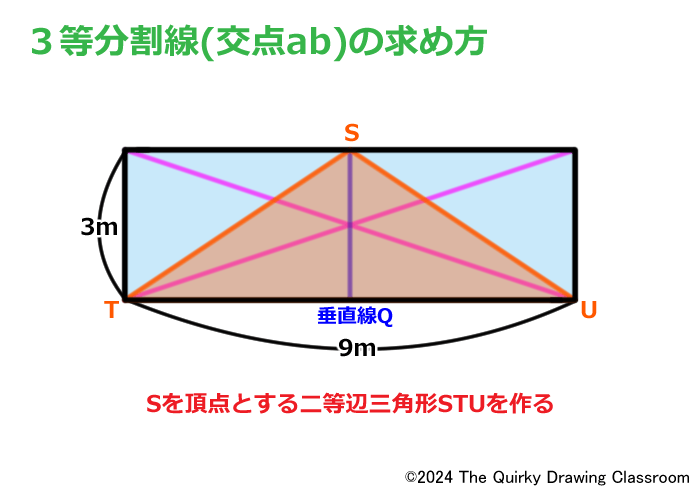
するとSを頂点とした二等辺三角形STUができあがります。
3等分割ではこの二等辺三角形と対角線から必要な分割位置を求めることができます。
二等辺三角形の2辺S-TとS-Uは対角線との間に交点を作っています。
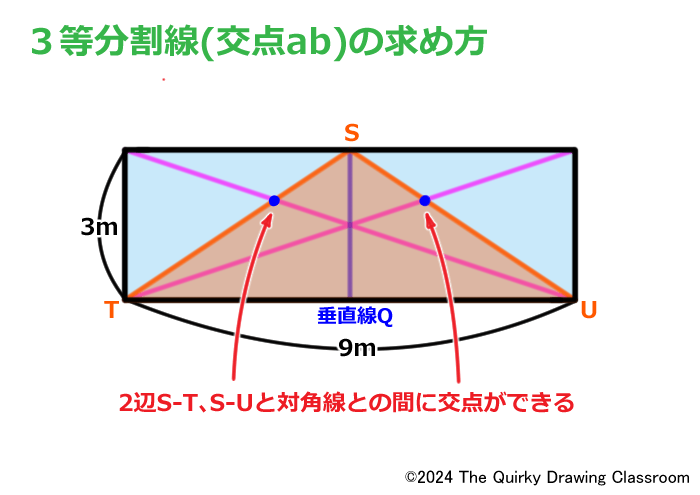
この交点が求めるべき交点a、bとなります。
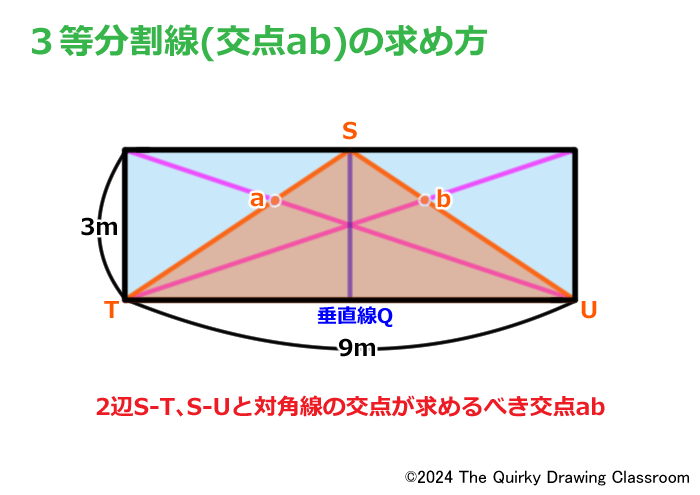
交点a、bを通る2本の垂直線A、Bを引くと長方形が3等分割されます。
これも元のパースのついた板に当てはめてみましょう。
するとこのようになります。
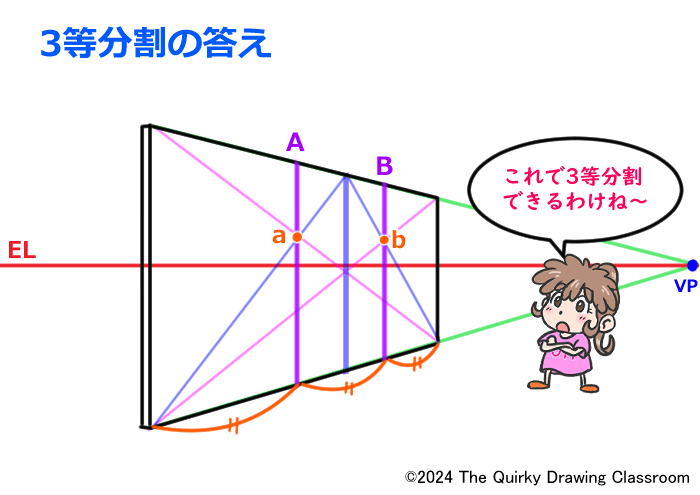
以上がパースのついた板を3等分割する方法です。
3等分割するためには、元の長方形を一度2等分割してから二等辺三角形を求め、その二等辺三角形の2辺と長方形の対角線が交わる交点を使ってユニットの分割をおこないます。
2等分割に比べると、少々手間がかかるのが3等分割です。
ただ、3等分割はまだ簡単な方で、これが5等分割になるともっとたくさんの補助線を引くことになります。
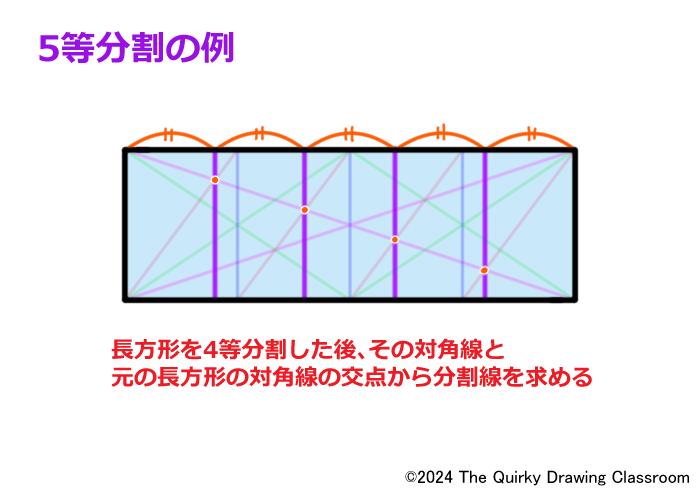
ユニットを偶数に分けるのは比較的簡単なのですが、奇数に分ける時がやっかいなのです。
とはいえ、これらの補助線の引き方をいちいちおぼえるのはとても大変です。
しかし、この問題を簡単に解決する分割のやり方があります。
これを次の項で解説します。
とても簡単に3等分割する方法
ユニットの奇数分割は偶数に分けるのに比べて手順が増えて大変です。
しかし、パースのユニット分割にはとても簡単な方法があります。
これは偶数、奇数関係なく簡単に分割できる方法です。
今回の記事はここが一番重要なポイントとなります。
では、やり方を解説していきます。
先ほど描いた3等分割の長方形に交点a、b、c、dを通る水平線を描き加えてみましょう。
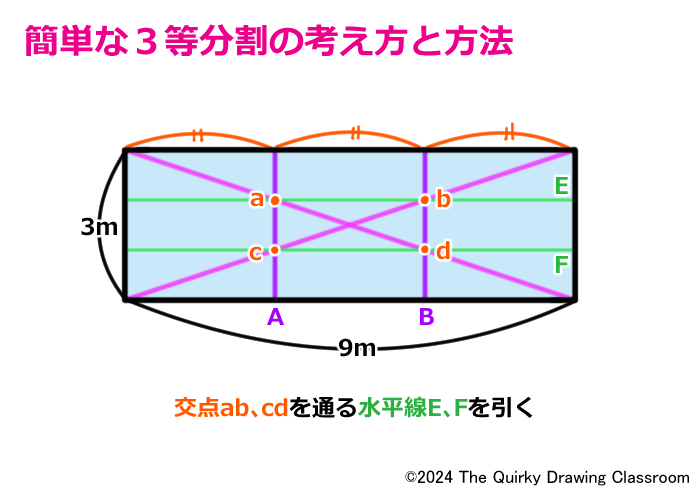
この2本の水平線をそれぞれE、Fとします。
この水平線E、Fを見ると、長方形を縦に3等分割する垂直線A、Bと同じ交点a、b、c、dで交わっていることがわかるかと思います。
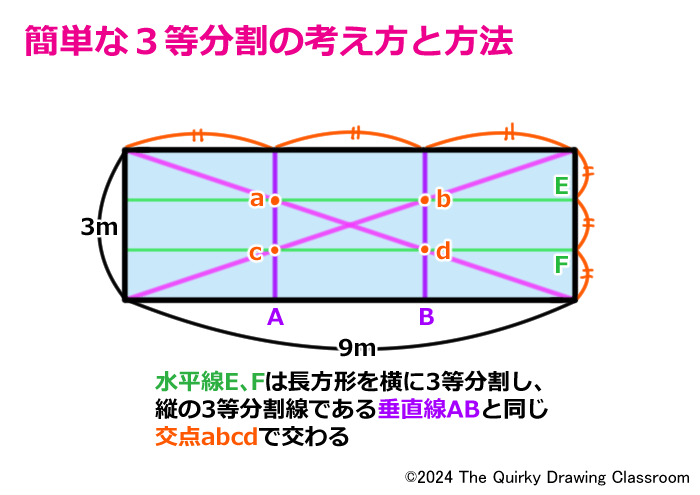
このことから水平線E、Fは、この長方形を横に3等分割する線であることもわかります。
つまり、ユニットを横に分割する水平線と対角線を使って、ユニットを縦に分割する垂直線を求めることができるのです。
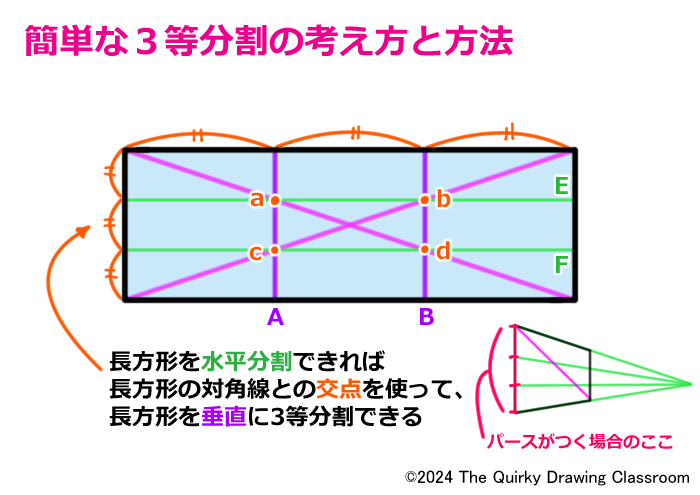
この方法の便利なところは5等分割でも、7等分割でも必要に応じたユニットの分割が可能になるところです。
もちろん、この性質はパースがついても変わりません。
例としてこの簡単な方法で板を5等分割してみましょう。
最初に基準となる板の1辺を5等分割します。
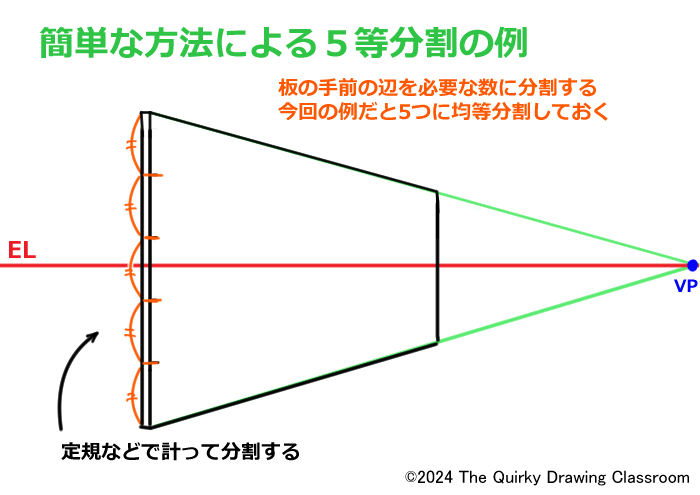
わかりやすいので、今回は手前の辺を5等分割しておきます。
ユニットに奥行きのパースがついている今回のような場合なら、縦方向の分割は定規などで計って必要な数に分割するだけです。
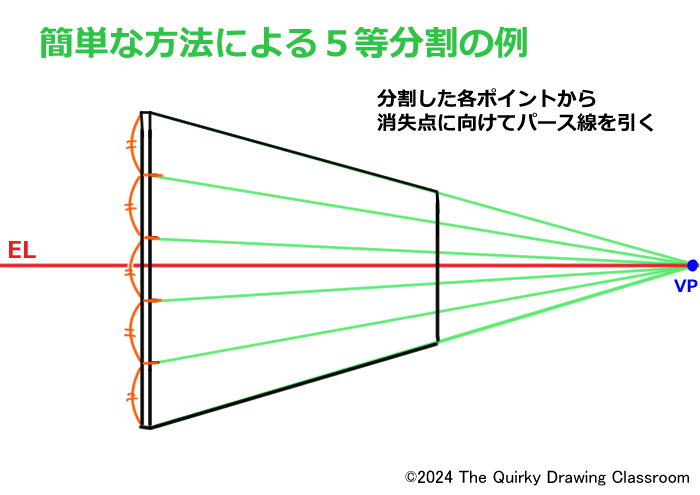
平面図で描いた水平分割線は、ここでは消失点(VP)へと収束するパース線となります。
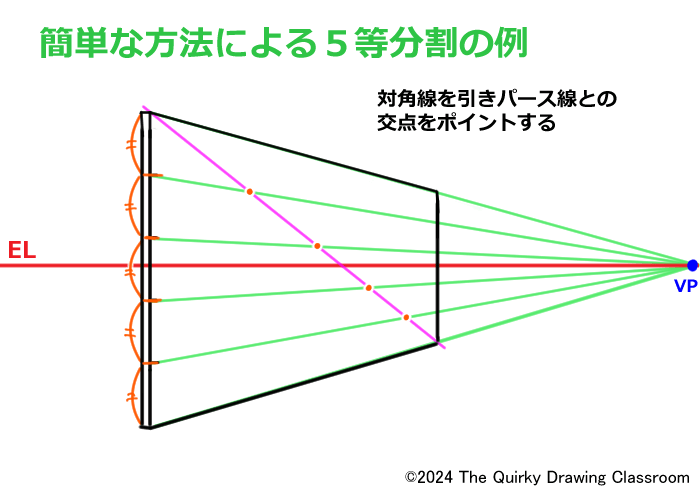
パース線を引いたら対角線を引いて、パース線との交点を求めます。
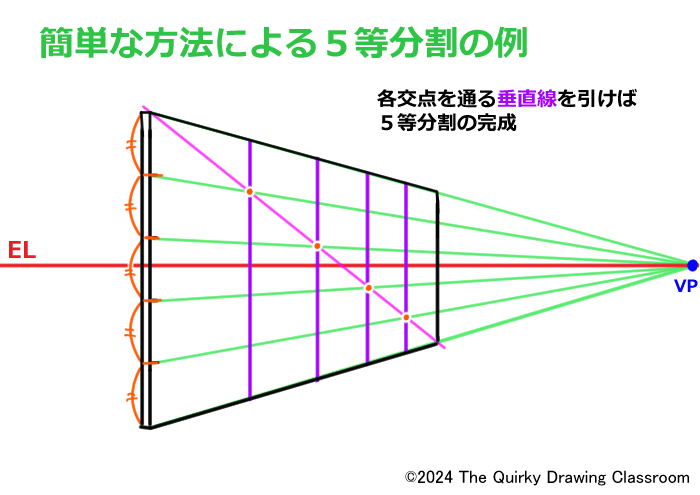
各交点を通る垂直線を引けば、板の5等分割の完成です。
これまで色々と説明してきましたが、パースの分割については、この対角線とパース線(水平分割線)の交点を使った分割方法を知っているだけでOKです。
これさえ知っていれば「分割」は十分に使いこなすことができます。
実用例:分割でブロック塀を描いてみよう
では、今までの分割の知識を使って例題に挑戦してみましょう。
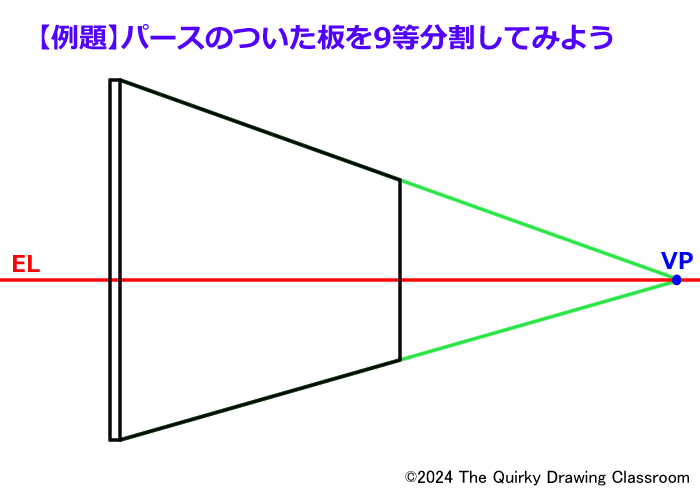
これは最初と同じような板ですが、この板を縦横9個のブロックで構成されるブロック塀にするにはどうすれば良いでしょうか?
ブロックは同じサイズのものを縦に9個積んでゆき、さらに同じものを9列ならべるものとします。
今回解説した簡単なユニット分割方法を使って描いてみて下さい。
答えはこの記事の一番最後に載せておきます。
▼初心者にもおすすめのパース学習用参考書はこちらから▼
パースの知識を身につけるためには、お手本を見ながら実際に描くのが一番です。
古本でも良いのでパースの参考書を何冊か手元に置いておくのがおすすめです。
要点まとめ
では、最後に要点をまとめておきます。
今回の要点はひとつだけです。
長々と解説してきましたが、おぼえておくべきはこの基準となる辺を必要な数に分割し、パース線と対角線を使ってユニット分割する方法です。
ただ「なぜそうなるか?」という理由も説明できるくらいまでになっておくと、知識として確実に定着したと言えるので、理屈も良ければしっかりとおさえておくと良いでしょう。
次回はパースを使った実用的な知識の第2弾「増殖」について解説します。
「増殖」は「分割」の反対の作業です。
分割はユニットを等しく分ける作業でしたが、増殖は最初のユニットと同じサイズのユニットを増やしてゆく作業となります。
「分割」と合わせて知っておくと、街などを描く時に有効活用できる知識です。
それでは、また次回。
【広告】▼「分割」も含めたパースの勉強におすすめの本▼
アメリカの画家ルーミスの名著『初めてのイラスト教室』の再編集復刊版。
ルーミス自身の説明図に加え、復刊にあたりより詳しい日本語版の解説図が追加されています。パースの基礎から応用まで幅広く学ぶことができるおすすめの1冊です。
例題の答え
上で出した例題の答えです。
まず、一番手前の基準となる辺を9個に分割し、消失点に向けてパース線(水平分割線)を引きます。
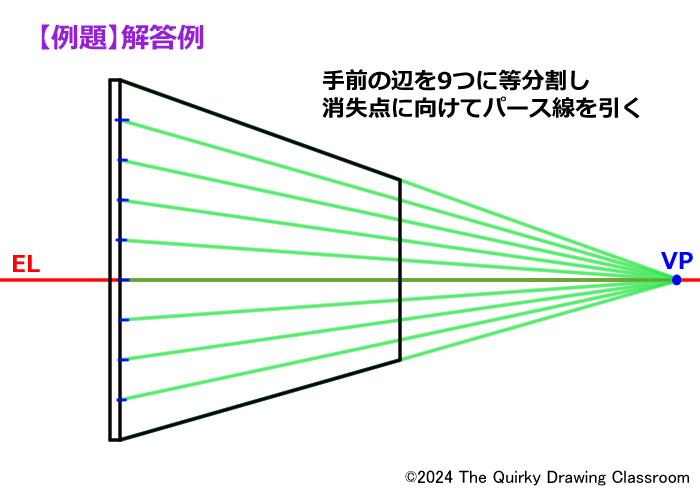
板の対角線を引いて、分割するポイントとなる交点を求めます。
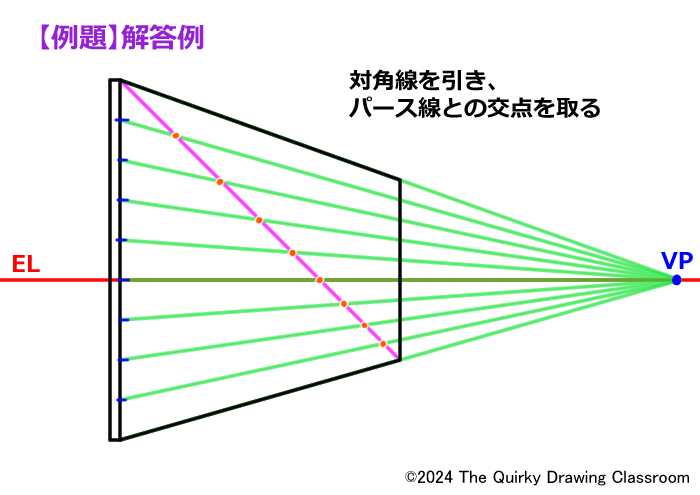
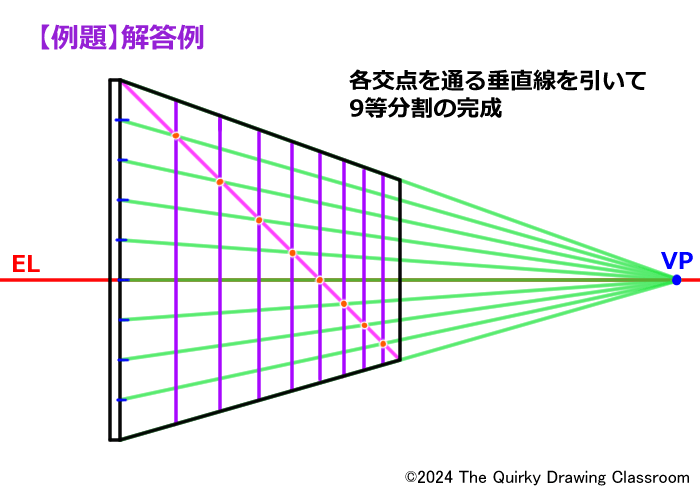
パース線と対角線の交点を通るように垂直線を描けば完成です。
▼少しでも勉強になったようでしたらクリックお願いします!
にほんブログ村